题目内容
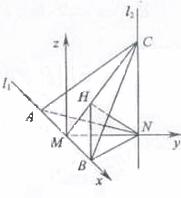
(20) 如图,l 
(Ⅰ)证明AC![]() ;
;
(Ⅱ)若![]() ,求NB与平面ABC所成角的余弦值.
,求NB与平面ABC所成角的余弦值.
解法一:
(1)由已知![]()
由已知![]() 可知AN=AB且AN⊥NB。
可知AN=AB且AN⊥NB。
又AN为AC在平面ABN内的射影。
∴AC⊥NB,
(Ⅱ)∵Rt△CNA≌Rt△CNB,
∴AC=BC,又已知∠ACB=600,因此△ABC为正三角形.
∵Rt△ANB≌Rt△CNB,
∴NC=NA=NB,因此N在平面ABC内的射影H是正三角形ABC的中心,连接BH,∠NBH为NB与平面ABC所成的角。
在Rt△NHB中,

解法二:
如图,建立空间直角坐标系M-xyz.
令MN=1,
则有A(-1,0,0),B(1,0,0),N(0,1,0).
(Ⅰ)∵MN是![]() 、
、![]() 的公垂线,
的公垂线,![]() ⊥
⊥![]() ,
,
∴![]() ⊥平面ABN,
⊥平面ABN,
∴![]() 平行于z轴.
平行于z轴.
故可设C(0,1,n)
于是![]()
![]()
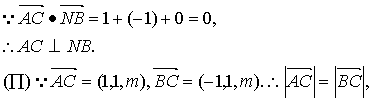
又已知∠ACB=60°,
∴△ABC为正三角形,AC=BC=AB=2.
在Rt△CNB中,NB=![]() ,可得NC=
,可得NC=![]() ,故C(0,1,
,故C(0,1,![]() ).
).
连结M![]() 作NH⊥MC于H,设H(
作NH⊥MC于H,设H(![]() )(
)(![]() >0)。
>0)。


练习册系列答案
相关题目
 如图所示,一个摩天轮半径为10 米,轮子的底部在地面上 2 米处,如果此摩天轮 20 秒转一圈,且当摩天轮上某人经过点 P 处(点尸与天轮中心 a 高度相同)开始计时(按逆时针方向转).
如图所示,一个摩天轮半径为10 米,轮子的底部在地面上 2 米处,如果此摩天轮 20 秒转一圈,且当摩天轮上某人经过点 P 处(点尸与天轮中心 a 高度相同)开始计时(按逆时针方向转). (2009•浦东新区一模)如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,
(2009•浦东新区一模)如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,
 (2013•湖南)在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”.如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”.某地有三个新建居民区,分别位于平面xOy内三点A(3,20),B(-10,0),C(14,0)处.现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心.
(2013•湖南)在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”.如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”.某地有三个新建居民区,分别位于平面xOy内三点A(3,20),B(-10,0),C(14,0)处.现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心.