题目内容
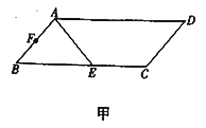
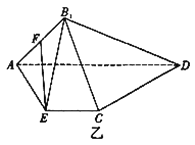
【题目】已知平面![]() 平面ABC,P、P在平面ABC的同侧,二面角
平面ABC,P、P在平面ABC的同侧,二面角![]() 的平面角为钝角,Q到平面ABC的距离为
的平面角为钝角,Q到平面ABC的距离为![]() ,
,![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() ,
,![]() ,
,![]() .
.
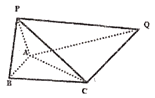
(1)求证:面![]() 平面PAB;
平面PAB;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由正弦定理,可求得![]() ,即
,即![]() ,再由平面
,再由平面![]() 平面ABC,可得
平面ABC,可得![]() 平面PAB,可证得面
平面PAB,可证得面![]() 平面PAB;
平面PAB;
(2)以A为坐标原点,![]() ,
,![]() 方向为x轴、y轴的正方向,建立空间直角坐标系.
方向为x轴、y轴的正方向,建立空间直角坐标系.
求出平面ACQ, 平面PAC的法向量,即可求得二面角.
(1)![]() ,
,
所以![]() ,
,![]()
![]() ,
,
又![]() 平面
平面![]() 平面ABC,
平面ABC,![]() 平面
平面![]() ,
,
![]() 平面ABC,
平面ABC,![]() 平面PAB,
平面PAB,![]() 面PAC,
面PAC,
![]() 面
面![]() 面PAB
面PAB
(2)以A为坐标原点,![]() ,
,![]() 方向为x轴、y轴的正方向,建立空间直角坐标系.
方向为x轴、y轴的正方向,建立空间直角坐标系.
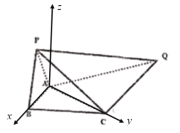
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面ACQ的法向量为![]() ,则
,则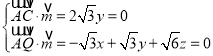 ,
,
令![]() ,
,![]()
设平面PAC的法向量为![]() ,则
,则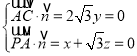 ,
,
令![]() :
:![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() .
.
而此二面角为锐角,故二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目