题目内容
（2012•绵阳一模）在△ABC中，角A，B，C的对边分别是a，b，c，若asinA=（a-b）sinB+csinC，
（I）求角C的值：
（II） 若c=2，且sinC+sin（B-A）=3sin2A，求△ABC的面积．
（I）求角C的值：
（II） 若c=2，且sinC+sin（B-A）=3sin2A，求△ABC的面积．
分析：（1）通过正弦定理化简表达式，利用余弦定理求出C的大小．
（2）通过三角形的内角和，以及两角和的正弦函数，以及sinC+sin（B-A）=3sin2A，推出cosA=0，判断三角形的形状，求出a，b的值，然后求解三角形的面积．
（2）通过三角形的内角和，以及两角和的正弦函数，以及sinC+sin（B-A）=3sin2A，推出cosA=0，判断三角形的形状，求出a，b的值，然后求解三角形的面积．
解答：解：（Ⅰ）∵asinA=（a-b）sinB+csinC，
由正弦定理
=
=
，得a2=（a-b）b+c2，
即a2+b2-c2=ab．①
由余弦定理得cosC=
=
，
结合0＜C＜π，得C=
． …（6分）
（Ⅱ）由 C=π-（A+B），得sinC=sin（B+A）=sinBcosA+cosBsinA，
∵sinC+sin（B-A）=3sin2A，
∴sinBcosA+cosBsinA+sinBcosA-cosBsinA=6sinAcosA，
整理得sinBcosA=3sinAcosA． …（8分）
若cosA=0，即A=
时，△ABC是直角三角形，且B=
，
于是b=ctanB=2tan
=
，∴S△ABC=
bc=
． …（10分）
若cosA≠0，则sinB=3sinA，由正弦定理得b=3a．②
联立①②，结合c=2，解得a=
，b=
，
∴S△ABC=
absinC=
×
×
×
=
．
综上，△ABC的面积为
或
．…（12分）
由正弦定理
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
即a2+b2-c2=ab．①
由余弦定理得cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
结合0＜C＜π，得C=
| π |
| 3 |
（Ⅱ）由 C=π-（A+B），得sinC=sin（B+A）=sinBcosA+cosBsinA，
∵sinC+sin（B-A）=3sin2A，
∴sinBcosA+cosBsinA+sinBcosA-cosBsinA=6sinAcosA，
整理得sinBcosA=3sinAcosA． …（8分）
若cosA=0，即A=
| π |
| 2 |
| π |
| 6 |
于是b=ctanB=2tan
| π |
| 6 |
2
| ||
| 3 |
| 1 |
| 2 |
2
| ||
| 3 |
若cosA≠0，则sinB=3sinA，由正弦定理得b=3a．②
联立①②，结合c=2，解得a=
2
| ||
| 7 |
6
| ||
| 7 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 7 |
6
| ||
| 7 |
| ||
| 2 |
3
| ||
| 7 |
综上，△ABC的面积为
2
| ||
| 3 |
3
| ||
| 7 |
点评：本题考查正弦定理与余弦定理的应用，解三角形的指数，考查分析问题解决问题的能力，计算能力．
练习册系列答案
阅读快车系列答案
相关题目
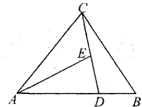（2012•绵阳一模）如图，在△ABC中，AD=2DB，DE=EC，若