题目内容
已知函数
，x∈[3，5]，则函数f（x）的最小值是 ．
【答案】分析：先利用反比例函数平移变换来判断函数在给定区间上的单调性，再求最小值．
解答：解：因为函数
在（-∞，0）上单调递增，在（0，+∞）上单调递减，
函数
可以看做由
向右平移一个单位，
所以函数
在（-∞，1）上单调递增，在（1，+∞）上单调递减，
所以函数在x=5时取得最小值，最小值为-1．
故答案为：-1．
点评：本题考察函数的最值求解，最值求解时易错为代端点值，所以求最值时关键是判断单调性．
解答：解：因为函数
在（-∞，0）上单调递增，在（0，+∞）上单调递减，函数
可以看做由向右平移一个单位，所以函数
在（-∞，1）上单调递增，在（1，+∞）上单调递减，所以函数在x=5时取得最小值，最小值为-1．
故答案为：-1．
点评：本题考察函数的最值求解，最值求解时易错为代端点值，所以求最值时关键是判断单调性．
练习册系列答案
相关题目
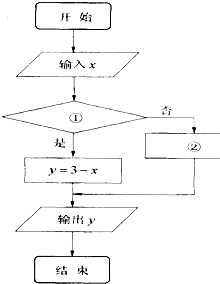已知函数y=|x-3|，如图，程序框图表示的是给定x值，求其相应函数值的算法．请将该程序框图补充完整，其中①处填