题目内容
计算:tan20°+2tan50°-tan70°.
【答案】分析:由两角差的正切公式,结合同角三角函数基本关系和诱导公式,化简得tan20°-tan70°=-2tan50°,由此可得
原式的值为0.
解答:解:∵tan(-50°)=tan(20°-70°)=
∴tan20°-tan70°=tan(-50°)(1+tan20°tan70°)
∵tan(-50°)=-tan50°,tan20°tan70°=tan20°cot20°=1
∴tan20°-tan70°=-2tan50°,因此可得
tan20°+2tan50°-tan70°=(tan20°-tan70°)+2tan50°=-2tan50°+tan50°=0
点评:本题求一个关于正切的式子的值,着重考查了诱导公式、同角三角函数的关系和两角差的正切公式等知识,属于基础题.
原式的值为0.
解答:解:∵tan(-50°)=tan(20°-70°)=

∴tan20°-tan70°=tan(-50°)(1+tan20°tan70°)
∵tan(-50°)=-tan50°,tan20°tan70°=tan20°cot20°=1
∴tan20°-tan70°=-2tan50°,因此可得
tan20°+2tan50°-tan70°=(tan20°-tan70°)+2tan50°=-2tan50°+tan50°=0
点评:本题求一个关于正切的式子的值,着重考查了诱导公式、同角三角函数的关系和两角差的正切公式等知识,属于基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
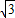 (tan10°+tan20°)= .
(tan10°+tan20°)= .
 tan20°-1)
tan20°-1) (tan10°+tan20°)= .
(tan10°+tan20°)= .