题目内容
已知四面体S-ABC中,SA⊥底面ABC,△ABC是锐角三角形,H是点A在面SBC上的射影.求证:H不可能是△SBC的垂心.
答案:
解析:
解析:
| 证明:假设H是△SBC的垂心,连结BH,并延长交SC于D点,则BH⊥SC
∵ AH⊥平面SBC, ∴ BH是AB在平面SBC内的射影 ∴ SC⊥AB(三垂线定理) 又∵ SA⊥底面ABC,AC是SC在面内的射影 ∴ AB⊥AC(三垂线定理的逆定理) ∴ △ABC是Rt△与已知△ABC是锐角三角形相矛盾,于是假设不成立. 故H不可能是△SBC的垂心.
|

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目

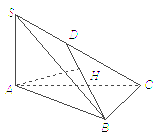 已知四面体S-ABC中,SA⊥底面ABC,△ABC是锐角三角形,H是点A在面SBC上的射影.求证:H不可能是△SBC的垂心.
已知四面体S-ABC中,SA⊥底面ABC,△ABC是锐角三角形,H是点A在面SBC上的射影.求证:H不可能是△SBC的垂心.