Question

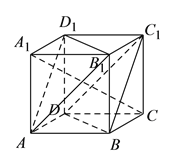
【题目】已知正方体．

求证：（ⅰ）面面．

（ⅱ）面．

Answer 1

【答案】（1）证明见解析；（2）证明见解析

【解析】试题分析：（1）由平行四边形的性质可得，由线面平行的判定定理可得平面，同理可得平面，从而根据面面平行的判定定理可得结论；（2）由三垂线定理得，同理，在根据线面垂直的判定定理可得结论.

试题解析：（ ）由正方的性质可知且,

∴是平行四边形，

∴,

又平面， 平面．

∴平面,

同理平面．

∴平面平面．

（）∵，

∴为在面内的射影，

∵，

∴由三垂线定理得，

同理，

∴平面．

【方法点晴】本题主要考查正方体的性质、线面垂直的判定定理及面面垂直的判定定理，属于难题.解答空间几何体中垂直关系时，一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化，转化时要正确运用有关的定理，找出足够的条件进行推理；证明直线和平面垂直的常用方法有：（1）利用判定定理；（2）利用判定定理的推论；（3）利用面面平行的性质；（4）利用面面垂直的性质，当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面.