题目内容
过双曲线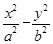
＝1(a>0，b>0)的左焦点F(－c,0)作圆x2＋y2＝a2的切线，切点为E，延长FE交抛物线y2＝4cx于点P，O为原点，若
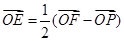，则双曲线的离心率为( )．
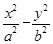＝1(a>0，b>0)的左焦点F(－c,0)作圆x2＋y2＝a2的切线，切点为E，延长FE交抛物线y2＝4cx于点P，O为原点，若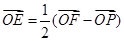，则双曲线的离心率为( )．A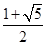． | B． | C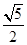． | D． |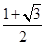
A
因为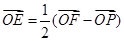，所以E是FP的中点．设双曲线的右焦点为F1，则F1也是抛物线的焦点．连接PF1，则|PF1|＝2a，且PF⊥PF1，所以|PF|＝
＝2b，设P(x，y)，过点F作x轴的垂线l，过点P作l的垂线，垂足为M，点P到该垂线的距离为2a，则x＋c＝2a，则x＝2a－c，在Rt△PMF中，由勾股定理得y2＋4a2＝4b2，即4c(2a－c)＋4a2＝4(c2－a2)，解得e＝.
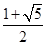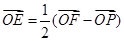，所以E是FP的中点．设双曲线的右焦点为F1，则F1也是抛物线的焦点．连接PF1，则|PF1|＝2a，且PF⊥PF1，所以|PF|＝＝2b，设P(x，y)，过点F作x轴的垂线l，过点P作l的垂线，垂足为M，点P到该垂线的距离为2a，则x＋c＝2a，则x＝2a－c，在Rt△PMF中，由勾股定理得y2＋4a2＝4b2，即4c(2a－c)＋4a2＝4(c2－a2)，解得e＝.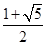
练习册系列答案
相关题目
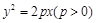的焦点为双曲线
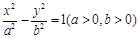的一个焦点，且两条曲线都经过点
.
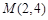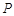在抛物线上，且它与双曲线的左，右焦点构成的三角形的面积为4，求点
＝2
，则直线l的斜率为________．
与椭圆
的离心率互为倒数，则双曲线的渐近线方程为（ ）
＝1(a>0，b>0)的一条渐近线与抛物线y＝x2＋1只有一个公共点，则双曲线的离心率为( )．
的右焦点为(3,0)，则该双曲线的离心率等于( )．
的渐近线方程是 .
是双曲线
的两个焦点，过点
的直线交双曲线
两点，若
为等边三角形，则双曲线
上的点，F1、F2是其焦点，且
，若△F1PF2的面积是9，a+b=7，则双曲线的离心率为（ ）
