题目内容
如图所示,圆柱底面的直径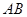 长度为
长度为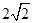 ,
,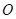 为底面圆心,正三角形
为底面圆心,正三角形 的一个顶点
的一个顶点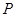 在上底面的圆周上,
在上底面的圆周上,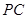 为圆柱的母线,
为圆柱的母线,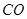 的延长线交
的延长线交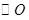 于点
于点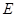 ,
, 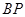 的中点为
的中点为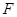 .
.
(1)
求证:平面 ⊥平面
⊥平面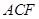 ;
;
(2)
求二面角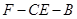 的正切值.
的正切值.
(1)见解析;(2)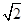 .
.
【解析】本试题主要考查了面面储值的判定和二面角的求解的综合运用。
解:(1)证明: 正三角形ABP中,F为BP的中点, ∴AF⊥PB …………1分
∵PC为圆柱的母线, ∴PC⊥平面ABC,
而AC在平面ABC内 ∴PC⊥AC ………………………………2分
∵AB为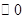 的直径,∴
的直径,∴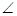 ACB=90°即 AC⊥BC ………………………………3分
ACB=90°即 AC⊥BC ………………………………3分
PC BC=C,∴AC⊥平面PBC,
………………………………………………4分
BC=C,∴AC⊥平面PBC,
………………………………………………4分
而PB在平面PBC内, ∴AC⊥PB ……………………………………5分
AC AF=A,∴PB⊥平面ACF,…………………………………………………6分
AF=A,∴PB⊥平面ACF,…………………………………………………6分
而PB在平面ABP内,∴平面ABP⊥平面ACF……………………………………7分
(2) 由(1)知AC⊥BC,PC⊥AC,同理PC⊥BC,
而PA=PB=PC=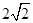 ,可证RT
,可证RT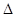 ABC≌RT
ABC≌RT PBC,
PBC,
∴AC=BC=PC=2……8分
以C为原点,CA,CB,CP所在直线为X,Y,Z轴建立空间直角坐标系
则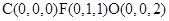 ……………………………9分
……………………………9分
∵PC⊥平面ABC,∴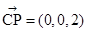 为平面CEB的一个法向量………………10分
为平面CEB的一个法向量………………10分
设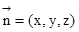 平面CEF的一个法向量,
平面CEF的一个法向量,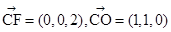
则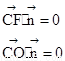 即
即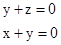 ,令y=-1则
,令y=-1则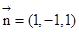 ……………………11分
……………………11分
设二面角F-CE-B的平面角为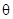 ,
,
∴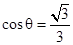 ……………………………………………12分
……………………………………………12分
∴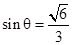 , ……………………………………………………………………13分
, ……………………………………………………………………13分
所以二面角F-CE-B的正切值为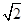 ………………………………………14分
………………………………………14分

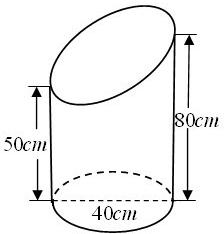
| A、2600cm2 | B、5200cm2 | C、2600πcm2 | D、5200πcm2 |
 圆柱形容器内部盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是
圆柱形容器内部盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是 (2012•茂名二模)如图所示,圆柱底面的直径AB长度为2
(2012•茂名二模)如图所示,圆柱底面的直径AB长度为2 如图所示,圆柱底面的直径AB长度为2
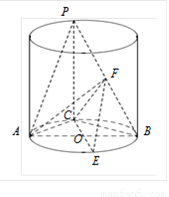
如图所示,圆柱底面的直径AB长度为2 ,O为底面圆心,正三角形ABP的一个顶点P在上底面的圆周上,PC为圆柱的母线,CO的延长线交⊙O于点E,BP的中点为F.
,O为底面圆心,正三角形ABP的一个顶点P在上底面的圆周上,PC为圆柱的母线,CO的延长线交⊙O于点E,BP的中点为F.