Question

已知椭圆方程为

x2

4

+

y2

3

=1，右焦点F（1，0），准线上一点C(4，3

3

)，过点F的直线l交椭圆与A、B两点．
（1）若直线l的倾斜角为

2

3

π，A点纵坐标为正数，求S_△CAF；
（2）证明直线AC和直线BC斜率之和为定值，并求此定值．

Answer 1

分析：（1）已知直线AF的斜率和点F（1，0），可以求出直线AF的方程，与椭圆方程联立，得出A的坐标，从而求出AF的长度，接着求出点C到直线AF的距离，再利用面积公式即可．
（2）讨论直线L的斜率．
①斜率为0时，方程为y=0，可以求出k_AC+K_BC=2

3

；
②斜率不为0时，令方程为x=my+1，与椭圆方程联立得到关于y的一元二次方程，再利用斜率公式分别求出直线AC和直线BC的斜率，相加后化简得到2

3

．综上所述，得到k_AC+k_BC=2

3

解答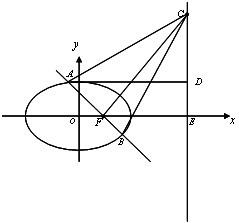：解：（1）利用点斜式易求出直线AF的方程：y=-

3

(x-1)，通过直线AF方程与椭圆方程联立得出A（0，

3

），即|AF|=2
点C到直线AF的距离d=

| 3 (4-1)+3 3 |

1+3

=3

3

S△ACF=

1

2

|AF|•d=3

3

．
（2）①若直线为y=0时，此时A（-2，0），B（2，0）．即k_AC+k_BC=2

3

②若直线不为y=0时，设直线l方程为x=my+1，

x=my+1 3x2+4y2-12=0

整理得：（3m²+4）y²+6my-9=0，△=36m²+36（3m²+4）＞0恒成立
设A（x₁，y₁），B（x₂，y₂）
∴y1+y2=-

6m

3m2+4

，y1y2=-

9

3m2+4

∵kAC=

3 3 -y1

4-x1

=

3 3 -y1

4-(my1+1)

=

3 3 -y1

3-my1

同理，kBC=

3 3 -y2

3-my2

∴kAC+kBC=

3 3 -y1

3-my1

+

3 3 -y2

3-my2

=

18 3 -(3+3 3 m)(y1+y2)+2my1y2

(3-my1)(3-my2)

=

18 3 -(3+3 3 m)( -6m 3m2+4 )+2m( -9 3m2+4 )

9-3m( -6m 3m2+4 )+m2( -9 3m2+4 )

=

72 3 m2+72 3

36m2+36

=2

3

∴直线AC与直线BC的斜率之和为定值2

3

．

点评：本题主要考查直线与椭圆综合题，考查椭圆的准线、焦点、直线的斜率等基础知识，但计算量比较大，一定细心，离不开平时的练习与努力．