题目内容
已知a≠0且a∈R,函数f(0)=asinx•cosx+| 2 |
| a |
| 2 |
| 1 |
| a |
(1)求函数g(a)的表达式;
(2)求函数g(a)的值域;
(3)找出所有使g(a)=g(
| 1 |
| a |
分析:(1)由函数的解析式知,求此函数的最值需要先用换元法转化,将此三角函数转化为一个一元二次函数在某一个区间上的最值问题.然后再用配方法求出函数的最值,由于本题中函数的对称轴不确定,属于二次函数最值中轴动区间定的问题,故本题需要对参数a的取值范围讨论,分类求函数的最小值.
(2)研究函数在每一段上的单调性,求出每一段上的值域,将其并起来既得函数的值域,研究函数单调性一般选择用导数法,此法较定义法简捷.
(3)依据g(a)的解析式在各段上探究g(a)=g(
)成立的a的值,方法是求解方程探究
(2)研究函数在每一段上的单调性,求出每一段上的值域,将其并起来既得函数的值域,研究函数单调性一般选择用导数法,此法较定义法简捷.
(3)依据g(a)的解析式在各段上探究g(a)=g(
| 1 |
| a |
解答:解:(1)令t=sinx+cosx,则t∈[-
,
],sinx•cosx=
,令m(t)=f(x).
则g(a)=m(t)min.则m(t)=f(x)=asinxcosx+
(sinx+cosx)=
+
t+
+
+2=
t2+
t+
+2
由题意知a≠0,m(t)=
(t2+
t)+
+2=
(t+
)2+2.
1°当-
<-
,即0<a<1时,m(t)在区间[-
,
]上单调递增,
∴g(a)=m(-
)=a+
.
2°当-
≤-
<0时,即a≥1时,m(t)min=m(-
)=2.
3°当0<-
≤
,即a≤-1时,m(t)min=m(-
)=a+
4°当-
>
,即-1<a<0时,m(t)min=m(-
)=a+
.
∴g(a)=
(2)当1>a>0时,N'(a)=(a+
)=1-
,令N'(a)=0得a=1.
当a∈(0,1)时,N'(a)<0,y(a)单调递减,
则a→0时,g(a)=a+
→+∞,∴g(a)≥2
当a<0时,由N'(a)=0有a=-1,且在(-∞,-1)上N'(a)>0在(-1,0)上N'(a)<0,
∴在a∈(-∞,0)上有g(a)≤g(-1)=-2,
∴g(a)值域为(-∞,-2]∪[2,+∞)
(3)若a>0,∵a•
=1,而当a∈(0,1)时g(a)>2,而a∈(1,+∞)时g(a)=2,
∴a>0时有且仅有a=1时有g(a)=g(
).
若a<0,a•
=1,∴a<-1,0>
>-1或-1<a<0,
<-1或a=
=-1,g(a)=a+
,g(
)=
+
=a+
∴总有g(a)=g(
).∴a<0时有g(a)=g(
).
综上有:a∈(-∞,0)∪{1}时有g(a)=g(
).
| 2 |
| 2 |
| t2-1 |
| 2 |
则g(a)=m(t)min.则m(t)=f(x)=asinxcosx+
| 2 |
| a(t2-1) |
| 2 |
| 2 |
| a |
| 2 |
| 1 |
| a |
| a |
| 2 |
| 2 |
| 1 |
| a |
由题意知a≠0,m(t)=
| a |
| 2 |
2
| ||
| a |
| 1 |
| a |
| a |
| 2 |
| ||
| a |
1°当-
| ||
| a |
| 2 |
| 2 |
| 2 |
∴g(a)=m(-
| 2 |
| 1 |
| a |
2°当-
| 2 |
| ||
| a |
| ||
| a |
3°当0<-
| ||
| a |
| 2 |
| 2 |
| 1 |
| a |
4°当-
| ||
| a |
| 2 |
| 2 |
| 1 |
| a |
∴g(a)=
|
(2)当1>a>0时,N'(a)=(a+
| 1 |
| a |
| 1 |
| a2 |
当a∈(0,1)时,N'(a)<0,y(a)单调递减,
则a→0时,g(a)=a+
| 1 |
| a |
当a<0时,由N'(a)=0有a=-1,且在(-∞,-1)上N'(a)>0在(-1,0)上N'(a)<0,
∴在a∈(-∞,0)上有g(a)≤g(-1)=-2,
∴g(a)值域为(-∞,-2]∪[2,+∞)
(3)若a>0,∵a•
| 1 |
| a |
∴a>0时有且仅有a=1时有g(a)=g(
| 1 |
| a |
若a<0,a•
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 | ||
|
| 1 |
| a |
∴总有g(a)=g(
| 1 |
| a |
| 1 |
| a |
综上有:a∈(-∞,0)∪{1}时有g(a)=g(
| 1 |
| a |
点评:本题考点是三角函数的最值,考查利用三角函数的恒等变换转化函数求最值,本题中函数结构复杂,求解时要分类讨论,分类讨论是一种重要的数学思想,其要义是通过分类是不确定变成确定,以达到求解问题的目的.本题中涉及到了用导数研究函数的单调性求值域,以及分类讨论求解方程成立的条件.本题难度较大,应细心严谨的进行探究.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
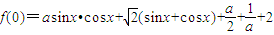 的最小值为g(a).
的最小值为g(a).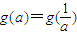 成立的实数a.
成立的实数a.