题目内容
(1)设扇形的周长是定值为c(c>0),中心角α.求证:当α=2时该扇形面积最大;
(2)设y=1-2a+a2-2acosx-2sin2x(-2≤a≤2,x∈R).求证:y≥-3.
(2)设y=1-2a+a2-2acosx-2sin2x(-2≤a≤2,x∈R).求证:y≥-3.
分析:(1)设扇形的弧长为l、半径为R,由扇形面积公式得到面积S关于l的函数,根据二次函数的性质算出当l=
时,S有最大值,进而算出此时的中心角α=2,使命题得证;
(2)利用同角三角函数的关系,将y化成关于a与cosx的式子,配方得y=2(cosx-
)2+
-2a-1,再由cosx的值域与a的范围加以计算,可得y的最小值
[(a-2)2-6]≥-3,从而得出y≥-3.
| c |
| 2 |
(2)利用同角三角函数的关系,将y化成关于a与cosx的式子,配方得y=2(cosx-
| a |
| 2 |
| a2 |
| 2 |
| 1 |
| 2 |
解答:解:(1)证明:设扇形的弧长为l、半径为R,可得2R+l=c,R=
(c>l).
∴扇形的面积S=
Rl=
•l=
(cl-l2)=-
(l-
)2+
.
∴当且仅当l=
时,S有最大值为
.
此时R=
,可得中心角α=
=2,
∴当α=2时该扇形面积最大,命题得证.
(2)证明:y=1-2a+a2-2acosx-2(1-cos2x),
=2(cosx-
)2+
-2a-1,
∵-2≤a≤2,可得-1≤
≤1,
∴当cosx=
时,ymin=
-2a-1=
[(a-2)2-6].
又∵-2≤a≤2,
∴ymin=
[(a-2)2-6]≥-3,当a=2时取等号,
即y≥-3,命题得证.
| c-l |
| 2 |
∴扇形的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| c-l |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| c |
| 2 |
| c2 |
| 16 |
∴当且仅当l=
| c |
| 2 |
| c2 |
| 16 |
此时R=
| c |
| 4 |
| l |
| R |
∴当α=2时该扇形面积最大,命题得证.
(2)证明:y=1-2a+a2-2acosx-2(1-cos2x),
=2(cosx-
| a |
| 2 |
| a2 |
| 2 |
∵-2≤a≤2,可得-1≤
| a |
| 2 |
∴当cosx=
| a |
| 2 |
| a2 |
| 2 |
| 1 |
| 2 |
又∵-2≤a≤2,
∴ymin=
| 1 |
| 2 |
即y≥-3,命题得证.
点评:本题证明了关于扇形与二次函数的命题成立,着重考查了扇形的弧长与面积公式、同角三角函数的基本关系和二次函数的图象与性质等知识,属于中档题.

练习册系列答案
相关题目
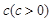 ,中心角
,中心角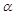 .求证:当
.求证:当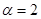 时该扇形面积最大;
时该扇形面积最大;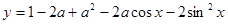
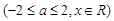 .求证:
.求证: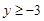 .
.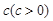 ,中心角
,中心角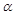 .求证:当
.求证:当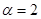 时该扇形面积最大;
时该扇形面积最大;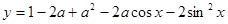
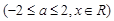 .求证:
.求证: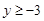 .
.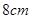 ,面积为
,面积为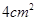 ,则扇形的圆心角的弧度数是
,则扇形的圆心角的弧度数是