题目内容
(1)设扇形的周长是定值为![]() ,中心角
,中心角![]() .求证:当
.求证:当![]() 时该扇形面积最大;
时该扇形面积最大;
(2)设![]() (-2≤a≤2,x∈R).求证:y≥-3.
(-2≤a≤2,x∈R).求证:y≥-3.
1)证明:设弧长为l,半径为R,则2R+l=c,![]() (
(![]() )----2分
)----2分
![]()
![]() -------------------------------------------------------5分
-------------------------------------------------------5分
此时![]() ,而
,而![]()
所以当![]() 时该扇形面积最大---------------------------------------7分
时该扇形面积最大---------------------------------------7分
(2)证明:![]()
![]() -----------------------------------------9分
-----------------------------------------9分
∵-2≤a≤2,∴-1≤![]() ≤1,--------------------------------------------11分
≤1,--------------------------------------------11分
∴当![]() 时,
时,![]()
![]() ---------14分
---------14分
又∵-2≤a≤2,∴![]() ≥-3,当a = 2时取等号,
≥-3,当a = 2时取等号,
即y≥-3.-------------------------------------------------------------------16分
法二:![]()
![]() ----------------------------9分
----------------------------9分
∵0≤![]() ≤2,-2≤a≤2,-------------------------------------------11分
≤2,-2≤a≤2,-------------------------------------------11分
∴当a=![]() 时,
时,
![]() ,--------------------14分
,--------------------14分
又∵-1≤![]() ≤1,∴
≤1,∴![]() ≥-3
≥-3
当![]() =1时取等号
=1时取等号
即y≥-3.-------------------------------------------------------------------16分

练习册系列答案
相关题目
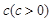 ,中心角
,中心角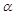 .求证:当
.求证:当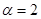 时该扇形面积最大;
时该扇形面积最大;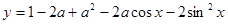
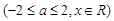 .求证:
.求证: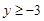 .
.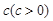 ,中心角
,中心角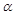 .求证:当
.求证:当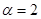 时该扇形面积最大;
时该扇形面积最大;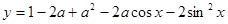
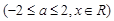 .求证:
.求证: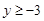 .
.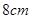 ,面积为
,面积为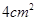 ,则扇形的圆心角的弧度数是
,则扇形的圆心角的弧度数是