题目内容
若F1、F2分别为双曲线(1)求此双曲线的离心率;
(2)若此双曲线过N(![]() ,2),求此双曲线的方程;
,2),求此双曲线的方程;
(3)若过N(![]() ,2)的双曲线的虚轴端点分别为B1、B2(B2在x轴正半轴上),点A、B在双曲线上,且
,2)的双曲线的虚轴端点分别为B1、B2(B2在x轴正半轴上),点A、B在双曲线上,且![]() =μ
=μ![]() ,求
,求![]() ⊥
⊥![]() 时直线AB的方程.
时直线AB的方程.
解:(1) ![]() =
=![]()
![]()
![]() =
=![]() ,∴PF1OM为平行四边形.
,∴PF1OM为平行四边形.
又![]() =λ(
=λ(![]() +
+![]() )知M在∠PF1O的角平分线上,
)知M在∠PF1O的角平分线上,
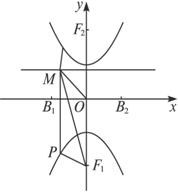
∴四边形PF1OM为菱形,且边长为|![]() |=|
|=|![]() |=c.
|=c.
∴|![]() |=2a+|
|=2a+|![]() |=2a+c.
|=2a+c.
由第二定义知![]() =e,即
=e,即![]() =e.
=e.
∴![]() +1=e且e>1
+1=e且e>1![]() e=2.
e=2.
(2)由e=2,∴c=2a,即b2=3a2.
双曲线方程为![]() -
-![]() =1.
=1.
又(3,2)在双曲线上,∴![]() -
-![]() =1.
=1.
∴a2=3.∴双曲线方程为![]() -
-![]() =1.
=1.
(3)由![]() =μ
=μ![]() 知AB过点B2,若AB⊥x轴,即lAB:x=3,此时AB1与BB1不垂直.
知AB过点B2,若AB⊥x轴,即lAB:x=3,此时AB1与BB1不垂直.
设直线AB的方程为y=kx-3k,代入![]() -
-![]() =1,得(3k2-1)x2-18k2x+27k2-9=0.
=1,得(3k2-1)x2-18k2x+27k2-9=0.
由题知3k2-1≠0且Δ>0,即k2>![]() 且k2≠
且k2≠![]() .
.
设交点A(x1,y1),B(x2,y2),![]() =(x1+3,y1),
=(x1+3,y1),![]() =(x2+3,y2).
=(x2+3,y2).
∵![]() ⊥
⊥![]() ,∴
,∴![]() ·
·![]() =0,即x1x2+3(x1+x2)+9+y1y2=0.
=0,即x1x2+3(x1+x2)+9+y1y2=0.
此时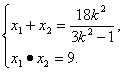
y1·y2=k2(x1-3)(x2-3)
=k2[x1x2-3(x1+x2)+9]
=k2(18-![]() )=
)=![]() .
.
∴9+3![]() +9+
+9+![]() =0.
=0.
∴5k2=1.∴k=±![]() .
.
∴直线AB的方程为y=![]() x-
x-![]() 或y=-
或y=-![]() x+
x+![]() .
.

练习册系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )