题目内容
设等差数列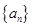 的前
的前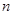 项和为
项和为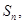
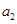 、
、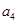 是方程
是方程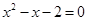 的两个根,则
的两个根,则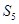 等于( )
等于( )
A.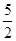 | B.5 | C.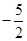 | D.-5 |
A
解析试题分析:因为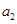 、
、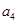 是方程
是方程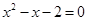 的两个根,所以
的两个根,所以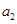 +
+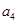 =1,所以
=1,所以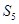


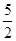 。
。
考点:等差数列的简单性质;等差数列前n项和公式的灵活应用;韦达定理。
点评:熟练掌握等差数列的简单性质是做本题的前提条件。

练习册系列答案
相关题目
设Sn是等差数列{an}的前n项和,若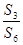 =
=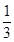 ,则
,则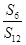 = ( )
= ( )
A.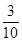 | B.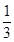 | C. | D. |
设Sn是等差数列{an}的前n项和,a12=-8,S9=-9,则S16= ( )
| A.-72 | B.72 | C.36 | D.-36 |
等差数列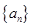 的前n项和为
的前n项和为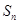 ,已知
,已知 ,
,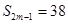 ,则
,则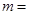 ( )
( )
| A.38 | B.20 | C.10 | D.9 |
在等差数列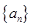 中,已知
中,已知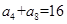 ,则该数列前11项和
,则该数列前11项和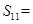
| A.58 | B.88 | C.143 | D.176 |
在等差数列3,7,11 …中,第5项为
| A.15 | B.18 | C.19 | D.23 |
等差数列中,若a3+a4+a5+a6+a7+a8+a9=420,则a2+a10=( )
| A.100 | B.120 | C.140 | D. 160 |
等差数列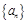 中,若
中,若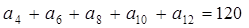 ,则
,则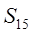 的值为:
的值为:
| A.180 | B.240 | C.360 | D.720 |
 个点,相应的图案中总的点数记为
个点,相应的图案中总的点数记为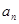 ,则
,则 ( )
( )






