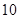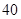题目内容
等差数列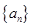 的前n项和为
的前n项和为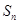 ,已知
,已知 ,
,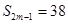 ,则
,则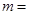 ( )
( )
| A.38 | B.20 | C.10 | D.9 |
C
解析试题分析:因为 ,所以由等差数列项性质得:
,所以由等差数列项性质得: ,当
,当 时不满足
时不满足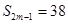 ,所以舍去;当
,所以舍去;当 时,由
时,由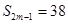 得,
得, ,所以
,所以 。
。
考点:等差数列的性质;等差数列前n项和的性质。
点评:熟练应用等差数列的性质:若 。属于基础题型。
。属于基础题型。

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
在等差数列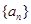 中,若
中,若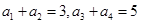 ,则
,则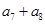 的和等于 ( )
的和等于 ( )
| A.7 | B.8 | C.9 | D.10 |
已知等差数列{an}满足a2=3,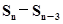 =51(n>3) ,
=51(n>3) ,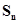 = 100,则n的值为
= 100,则n的值为
| A.8 | B.9 | C.10 | D.11 |
设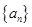 是等差数列,且
是等差数列,且 ,则这个数列的前5项和
,则这个数列的前5项和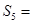 ( )
( )
| A.10 | B.15 | C.20 | D.25 |
等差数列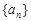 中,a3="7," a9=19,则a5= ( )
中,a3="7," a9=19,则a5= ( )
| A.10 | B.11 | C.12 | D.13 |
设等差数列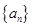 的前
的前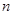 项和为
项和为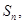
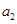 、
、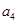 是方程
是方程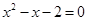 的两个根,则
的两个根,则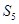 等于( )
等于( )
A.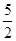 | B.5 | C.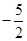 | D.-5 |
已知等差数列 的前
的前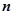 项和为
项和为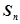 ,且满足
,且满足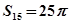 ,则
,则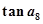 的值是( )
的值是( )
A. | B.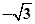 | C.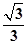 | D.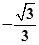 |
等差数列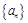 中,若
中,若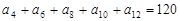 ,则
,则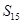 的值为: ( )
的值为: ( )
| A.180 | B.240 | C.360 | D.720 |
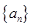 的前项和为
的前项和为 ,若
,若 三点共线,
三点共线, 为坐标原点,且
为坐标原点,且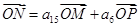 (直线
(直线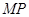 不过点
不过点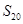 等于 ( )
等于 ( )