题目内容
如图,四棱柱 的底面
的底面 是平行四边形,且
是平行四边形,且 底面
底面 ,
, ,
, ,
, °,点
°,点 为
为 中点,点
中点,点 为
为 中点.
中点.

(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)设二面角 的大小为
的大小为 ,直线
,直线 与平面
与平面 所成的角为
所成的角为 ,求
,求 的值.
的值.
【答案】
(Ⅰ)证明详见解析;(Ⅱ)
【解析】
试题分析:(Ⅰ)由已知条件可求得 ,
, ,所以
,所以 ,即
,即 ,
, 底面
底面 ,
, ,根据平面与平面垂直的判定定理可得平面
,根据平面与平面垂直的判定定理可得平面 平面
平面 .(Ⅱ)由(Ⅰ)可知
.(Ⅱ)由(Ⅰ)可知


 ,所以
,所以 为二面角
为二面角 的平面角,即
的平面角,即 ,
,
 .过
.过 作
作 的垂线,垂足为
的垂线,垂足为 ,连结
,连结 ,则
,则 为直线
为直线 与平面
与平面 所成的角,可证得
所成的角,可证得 ,
, ,所以
,所以 ,即
,即 .
.
试题解析:【解】(1) ,
, ,
, ,又
,又 ,
, ,则
,则 ,即
,即 .又
.又 底面
底面 ,
, ,而
,而 则
则 平面
平面 ,又
,又 平面
平面 ,
,
 平面
平面 平面
平面 .
5分
.
5分
(2) 为二面角
为二面角 的平面角,则
的平面角,则 ,
, .
7分
.
7分
过 作
作 的垂线,垂足为
的垂线,垂足为 ,连结
,连结 ,又
,又 平面
平面 ,
, ,则
,则 平面
平面 ,
, 为直线
为直线 与平面
与平面 所成的角,
9分
所成的角,
9分
易得 ,
, ,
11分
,
11分
则 ,即
,即 .
12分
.
12分
考点:1.平面与平面垂直的判断;2.二面角和直线与平面的夹角;3.诱导公式和三角函数的性质.

练习册系列答案
相关题目
 的底面
的底面 是平行四边形,
是平行四边形, 分别在棱
分别在棱 上,且
上,且 .
. ;
; 平面
平面 是边长为
是边长为 的正方形,且
的正方形,且 ,
, ,求线段
,求线段 的长, 并证明:
的长, 并证明:

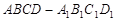 的底面是边长为
的底面是边长为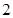 的正方形,
的正方形,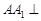 底面
底面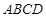 ,
, ,点
,点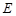 在棱
在棱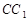 上,点
上,点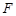 是棱
是棱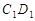 的中点
的中点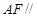 平面
平面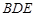 时,求
时,求 的长;
的长;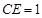 时,求二面角
时,求二面角 的余弦值。
的余弦值。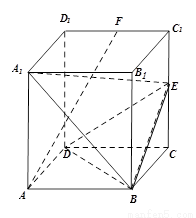
 的底面是正方形,侧棱
的底面是正方形,侧棱 平面
平面  ,且
,且 ,则异面直线
,则异面直线 所成角的余弦值为(
)
所成角的余弦值为(
)
 B.
B.  C.
C.  D.
D.

 (1)当
(1)当