题目内容
已知直线l的参数方程：
（t为参数）和圆C的极坐标方程：ρ=2
sin(θ+
)．
（Ⅰ）将直线l的参数方程化为普通方程，圆C的极坐标方程化为直角坐标方程；
（Ⅱ）判断直线l和圆C的位置关系．
|
| 2 |
| π |
| 4 |
（Ⅰ）将直线l的参数方程化为普通方程，圆C的极坐标方程化为直角坐标方程；
（Ⅱ）判断直线l和圆C的位置关系．
（Ⅰ）消去参数t，得直线l的普通方程为y=2x+1，
ρ=2
sin(θ+
)，即ρ=2（sinθ+cosθ），
两边同乘以ρ得ρ2=2（ρsinθ+ρcosθ），
得⊙C的直角坐标方程为（x-1）2+（y-1）2=2；
（Ⅱ）圆心C到直线l的距离d=
=
＜
，
所以直线l和⊙C相交．
ρ=2
| 2 |
| π |
| 4 |
两边同乘以ρ得ρ2=2（ρsinθ+ρcosθ），
得⊙C的直角坐标方程为（x-1）2+（y-1）2=2；
（Ⅱ）圆心C到直线l的距离d=
| |2-1+1| | ||
|
2
| ||
| 5 |
| 2 |
所以直线l和⊙C相交．
练习册系列答案
通城学典默写能手系列答案
相关题目
和
，则曲线C1与C2的交点坐标为_______。
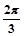,1)对应点的直角坐标是__________.
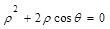,点P的极坐标为
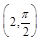,过点P作圆C的切线,则两条切线夹角的正切值是 
到定直线
的距离比到定点
的距离多1，
的方程；
，求曲线
到点
距离的最小值