题目内容
不同的直线m和n，不同的平面α，β，γ，下列条件中能推出α∥β的是（ ）
分析：利用平面平行的判定定理，对四个选项分别进行判断，能够得到正确答案．
解答：解：由不同的直线m和n，不同的平面α，β，γ，知：
若α∩γ=n，β∩γ=m，n∥m，则α与β相交或平行，故A不正确；
若α⊥γ，β⊥γ，则α与β相交或平行，故B不正确；
若n∥m，n⊥α，m⊥β，则由平面平行的判定定理知α∥β，故C正确；
若n∥α，m∥β，n∥m，则α与β相交或平行，故D不正确．
故选C．
若α∩γ=n，β∩γ=m，n∥m，则α与β相交或平行，故A不正确；
若α⊥γ，β⊥γ，则α与β相交或平行，故B不正确；
若n∥m，n⊥α，m⊥β，则由平面平行的判定定理知α∥β，故C正确；
若n∥α，m∥β，n∥m，则α与β相交或平行，故D不正确．
故选C．
点评：本题考查平面平行的判断所应用，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
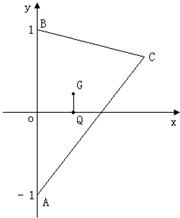设G，Q分别为△ABC的重心和外心，A（0，-1），B（0，1），且GQ∥AB．