题目内容
不同的直线m和n,不同的平面α,β,γ,下列条件中哪个是α∥β的充分不必要条件( )A.α∩γ=n,β∩γ=m,n∥m
B.α⊥γ,β⊥γ
C.n∥m,n⊥α,m⊥β
D.n∥α,m∥β,n∥m
【答案】分析:先根据线面平行、面面平行的判定与性质,在A、B、C、D各项中找出一个能使“α∥β”成立的一个条件,说明是充分条件,然后再在结果中找出反之不能成立的项,即可得出答案.
解答:解:对于A:由α∩γ=n,β∩γ=m,n∥m,不可以得出α∥β,故不是充分条件;
对于B:由α⊥γ,β⊥γ,不一定能得出α∥β,故不是充分条件;
对于C:由n∥m,n⊥α,m⊥β,可以得出α∥β,反之不一定成立;故是充分不必要条件;
对于D:由n∥α,m∥β,n∥m,有可能α与β相交,不能得出α∥β,故不是充分条件.
故选C.
点评:本题考查了立体几何中线面平行、面面平行的判定与性质,考查了面面平行与线线平行之间的转化关系.属于基本题.熟练掌握空间的线面、面面垂直的有关定理是解决本题的关键.
解答:解:对于A:由α∩γ=n,β∩γ=m,n∥m,不可以得出α∥β,故不是充分条件;
对于B:由α⊥γ,β⊥γ,不一定能得出α∥β,故不是充分条件;
对于C:由n∥m,n⊥α,m⊥β,可以得出α∥β,反之不一定成立;故是充分不必要条件;
对于D:由n∥α,m∥β,n∥m,有可能α与β相交,不能得出α∥β,故不是充分条件.
故选C.
点评:本题考查了立体几何中线面平行、面面平行的判定与性质,考查了面面平行与线线平行之间的转化关系.属于基本题.熟练掌握空间的线面、面面垂直的有关定理是解决本题的关键.

练习册系列答案
相关题目
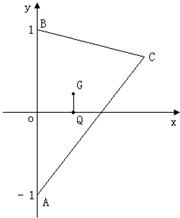 设G,Q分别为△ABC的重心和外心,A(0,-1),B(0,1),且GQ∥AB.
设G,Q分别为△ABC的重心和外心,A(0,-1),B(0,1),且GQ∥AB.