题目内容

2．若△ABC中，三边a，b，c满足a：b：c=3：5：x，且∠C=120°，则x=7．

分析 由a：b：c=3：5：x，设a=3k，b=5k，c=kx，（k＞0）．∠C=120°，kx＞5k．利用余弦定理求解即可．

解答 解：由题意：由a：b：c=3：5：x，设a=3k，b=5k，c=kx，（k＞0）．
∵∠C=120°，即kx＞5k．
由余弦定理可得：cos120°=$\frac{9{k}^{2}+25{k}^{2}-{k}^{2}{x}^{2}}{30{k}^{2}}$，
可得：$\frac{34-{x}^{2}}{30}=-\frac{1}{2}$，
解得：x=7．
故答案为：7．

点评 本题主要考查了余弦定理，三角形中大边对大角等知识的应用，属于基础题．

练习册系列答案
相关题目
13．在直角坐标系xOy中，直线l1的方程为y=$\sqrt{3}$x，曲线C的参数方程为$\left\{\begin{array}{l}x=1+\sqrt{3}cosφ\\ y=\sqrt{3}sinφ\end{array}$（φ是参数，0≤φ≤π）．以O为极点，x轴的非负半轴为极轴建立极坐标系．
（1）分别写出直线l1与曲线C的极坐标方程；
（2）若直线${l_2}：2ρsin（θ+\frac{π}{3}）+3\sqrt{3}$=0，直线l1与曲线C的交点为A，直线l1与l2的交点为B，求|AB|．
14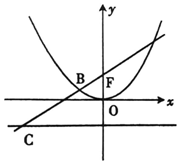．如图，过抛物线x2=2py（p＞0）的焦点F的直线l交抛物线于AB，交其准线于点C，若|BC|=2|BF|，且|AF|=2，则p=（　　）
A．1B．$\sqrt{2}$C．2D．2-$\sqrt{2}$
11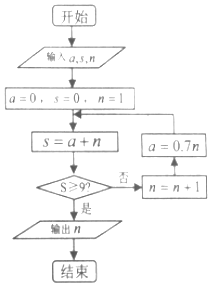．我国古代数学典籍《九章算术》“盈不足”中有一道问题：“今有垣高九尺，瓜生其上，蔓日长七寸；瓠生其下，蔓日长一尺，问几何日相逢？”现用程序框图描述，如图所示，则输出的结果n=（　　）
A．4B．5C．6D．7
18．在△ABC中，角A，B，C对应的边分别为a，b，c，已知a=4，b=5，cos（B-A）=$\frac{31}{32}$，则cosB=$\frac{9}{16}$．
7．E为正四面体D-ABC棱AD的中点，平面α过点A，且α∥平面ECB，α∩平面ABC=m，α∩平面ACD=n，则m、n所成角的余弦值为（　　）
A．$\frac{\sqrt{3}}{3}$B．$\frac{\sqrt{6}}{3}$C．$\frac{\sqrt{2}}{2}$D．$\frac{1}{3}$
14．给出下列命题：
①若函数y=f（x）满足f（x-1）=f（x+1），则函数f（x）的图象关于直线x=1对称；
②点（2，1）关于直线x-y+1=0的对称点为（0，3）；
③通过回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$可以估计和观测变量的取值和变化趋势；
④正弦函数是奇函数，f（x）=sin（x2+1）是正弦函数，所以f（x）=sin（x2+1）是奇函数，上述推理错误的原因是大前提不正确．
其中真命题的序号是②③．
11．已知等差数列{an}的公差d不为0，且${a_{k_1}}$，${a_{k_2}}$，…，${a_{k_n}}$，…（k1＜k2＜…＜kn＜…）成等比数列，公比为q．
（1）若k1=1，k2=3，k3=8，求$\frac{a_1}{d}$的值；
（2）当$\frac{a_1}{d}$为何值时，数列{kn}为等比数列；
（3）若数列{kn}为等比数列，且对于任意n∈N*，不等式${a_n}+{a_{k_n}}＞2{k_n}$恒成立，求a1的取值范围．
12．已知f（x）=|x+1|+|x-1|．
（Ⅰ）求不等式f（x）＜4的解集；
（Ⅱ）若不等式f（x）-|a-1|＜0有解，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网