题目内容
直线 绕原点按顺时针方向旋转
绕原点按顺时针方向旋转 所得直线与圆
所得直线与圆 的位置关系是( ).
的位置关系是( ).
| A.直线与圆相切 | B.直线与圆相交但不过圆心 |
| C.直线与圆相离 | D.直线过圆心 |
A
解析试题分析:直线 的斜率为
的斜率为 ,倾斜角为
,倾斜角为 ,绕原点按顺时针方向旋转
,绕原点按顺时针方向旋转 所得直线倾斜角为
所得直线倾斜角为 ,斜率为
,斜率为 ,所以直线方程为
,所以直线方程为 ,圆
,圆 的圆心到直线的距离
的圆心到直线的距离 ,正好等于圆半径,所以直线与圆相切.
,正好等于圆半径,所以直线与圆相切.
考点:本小题主要考查直线的倾斜角和斜率与直线和圆的位置关系的判断,考查学生分析问题解决问题的能力和运算求解能力.
点评:考查直线与圆的位置关系有代数法和几何法两种方法,用几何法比较简单,一般考虑用几何法,即考查圆心到直线的距离与半径的关系.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
将圆x2+y2 -2x-4y+1=0平分的直线是
| A. x+y-1=0 | B.x+y+3=0 | C.x-y+1=0 | D.x-y+3=0 |
若点 为圆
为圆 的弦
的弦 的中点,则直线
的中点,则直线 的方程为( )
的方程为( )
A. | B. |
C. | D. |
若直线 与曲线
与曲线 有公共点,则
有公共点,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
已知圆 与直线
与直线 及
及 都相切,圆心在直线
都相切,圆心在直线 上,则圆
上,则圆 的方程为( )
的方程为( )
A. | B. |
C. | D. |
动点在圆x2+y2=1上移动时,它与定点B(3,0)连线的中点轨迹方程是( )
| A.(x+3)2+y2=4 | B.(x-3)2+y2=1 |
| C.(2x-3)2+4y2=1 | D.(x+ )2+y2= )2+y2= |
过点(1,2)总可作两条直线与圆 相切,则实数
相切,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. 或 或 | D.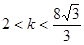 或 或 |
点 在圆
在圆 的内部,则
的内部,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. 或 或 | D. |
圆 :
: 与圆
与圆 公切线的条数是( )
公切线的条数是( )
| A.0条 | B.1条 | C.2条 | D.3条 |