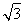Question

设函数f(x)=sin2x-sin(2x-

π

6

).
（1）求函数f（x）的值域；
（2）设A，B，C为△ABC的三个内角，若cosB=

1

3

，f(

C

2

)=-

1

4

，且C为锐角，求sinA的值．

Answer 1

分析：（1）利用二倍角公式对函数解析式化简整理，进而根据正弦函数的性质求得函数的值域．
（2）把x=

c

2

代入函数解析式，求得sinC，进而求得C，进而根据cosB，求得sinB，代入到sinA=sin（B+C）中求得答案．

解答：解：（1）f(x)=

1-cos2x

2

-

3

2

sin2x+

1

2

cos2x=

1

2

-

3

2

sin2x
所以函数f（x）的值域为[

1- 3

2

，

1+ 3

2

]．
（2）f(

C

2

)=

1

2

-

3

2

sinC=-

1

4

，所以sinC=

3

2

，
因为C为锐角，所以C=

π

3

.
又因为在△ABC中，cosB=

1

3

，所以sinB=

2

3

2

，
所以sinA=sin（B+C）=sinBcosC+cosBsinC=

2

3

2

×

1

2

+

1

3

×

3

2

=

2 2 + 3

6

.

点评：本题主要考查了二倍角的正弦．解题的关键是对二倍角公式的熟练掌握．