题目内容
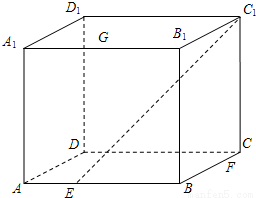
(理)已知正方体ABCD一A1B1C1D1的棱长为1,则BC1与DB1的距离为
- A.

- B.

- C.

- D.2

C
分析:连接BD1,BD1∩DB1=O,取C1D1的中点E,连接DE,EB1,则OE∥BC1,可得BC1∥平面DB1E,从而BC1与DB1的距离为BC1与平面DB1E的距离,即C1到平面DB1E的距离,利用等体积可求.
解答: 解:连接BD1,BD1∩DB1=O,取C1D1的中点E,连接DE,EB1,则OE∥BC1,
解:连接BD1,BD1∩DB1=O,取C1D1的中点E,连接DE,EB1,则OE∥BC1,
∵BC1?平面DB1E,OE?平面DB1E
∴BC1∥平面DB1E
∴BC1与DB1的距离为BC1与平面DB1E的距离,即C1到平面DB1E的距离
在△DB1E中,DE= ,EB1=
,EB1= ,DB1=
,DB1= ,EO=
,EO= ,
,
∴S△DB1E= =
=
设C1到平面DB1E的距离为d,则由VC1-DB1E=VD-B1C1E,可得 ×
× d=
d= ×
×
∴d=
故选C.
点评:本题考查线线距离,解题的关键是将BC1与DB1的距离为BC1与平面DB1E的距离,即C1到平面DB1E的距离,从而利用等体积求解.
分析:连接BD1,BD1∩DB1=O,取C1D1的中点E,连接DE,EB1,则OE∥BC1,可得BC1∥平面DB1E,从而BC1与DB1的距离为BC1与平面DB1E的距离,即C1到平面DB1E的距离,利用等体积可求.
解答:
 解:连接BD1,BD1∩DB1=O,取C1D1的中点E,连接DE,EB1,则OE∥BC1,
解:连接BD1,BD1∩DB1=O,取C1D1的中点E,连接DE,EB1,则OE∥BC1,∵BC1?平面DB1E,OE?平面DB1E
∴BC1∥平面DB1E
∴BC1与DB1的距离为BC1与平面DB1E的距离,即C1到平面DB1E的距离
在△DB1E中,DE=
 ,EB1=
,EB1= ,DB1=
,DB1= ,EO=
,EO= ,
,∴S△DB1E=
 =
=
设C1到平面DB1E的距离为d,则由VC1-DB1E=VD-B1C1E,可得
 ×
× d=
d= ×
×
∴d=

故选C.
点评:本题考查线线距离,解题的关键是将BC1与DB1的距离为BC1与平面DB1E的距离,即C1到平面DB1E的距离,从而利用等体积求解.

练习册系列答案
相关题目
 (2005•静安区一模)已知正方体ABCD-A1B1C1D1的棱长为2,点E、F分别在底面正方形的边AB、BC上,且
(2005•静安区一模)已知正方体ABCD-A1B1C1D1的棱长为2,点E、F分别在底面正方形的边AB、BC上,且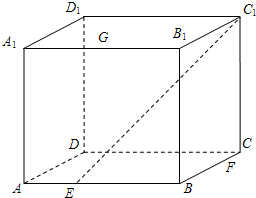 已知正方体ABCD-A1B1C1D1的棱长为2,点E、F分别在底面正方形的边AB、BC上,且
已知正方体ABCD-A1B1C1D1的棱长为2,点E、F分别在底面正方形的边AB、BC上,且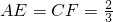 ,点G为棱A1B1的中点.
,点G为棱A1B1的中点.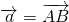 ,
,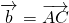 .当实数k为________时k
.当实数k为________时k 与k
与k 互相垂直.
互相垂直.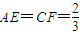 ,点G为棱A1B1的中点.
,点G为棱A1B1的中点.