题目内容
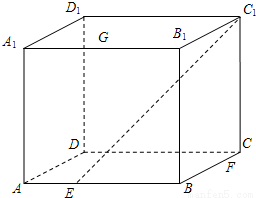
已知正方体ABCD-A1B1C1D1的棱长为2,点E、F分别在底面正方形的边AB、BC上,且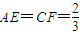 ,点G为棱A1B1的中点.
,点G为棱A1B1的中点.(1)在图中画出正方体过三点E、F、G的截面,并保留作图痕迹;
(2)(理)求(1)中的截面与底面ABCD所成锐二面角的大小.
(3)(文)求出直线EC1与底面ABCD所成角的大小.
【答案】分析:(1)由已知,EF∥A1C1,取B1C1中点H,EF∥GH,连接E,F,G,H,即为截面.
(2)建立空间直接坐标系,利用平面EFHG法向量与底面法向量夹角去求截面EFGH与底面ABCD所成锐二面角的大小.
(3))因为C1C⊥底面ABCD,所以∠C1EC就是所求的角.在RT△C1CE中 求解即可.
解答: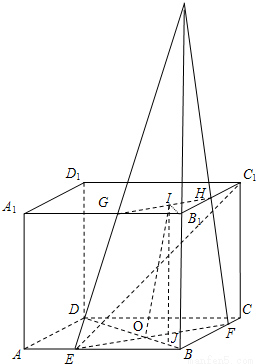 解:(1)如图,截面为EFHG
解:(1)如图,截面为EFHG
(2)如图,建空间直角坐标系,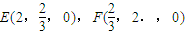 ,
,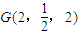 ,
,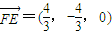 ,
,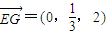 (8分)
(8分)
平面EFHG法向量为(-6,-6,1),底面法向量为(0,0,1)
设向量夹角θ,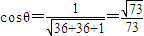 (12分)
(12分)
截面EFHG与底面所成锐二面角大小为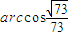 (14分)
(14分)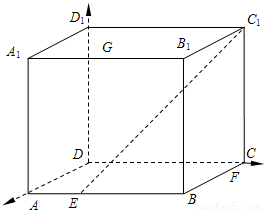
(3)∵C1C⊥底面ABCD,∴∠C1EC就是所求的角 (9分)
在RT△C1CE中,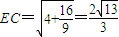 ,
, (12分)
(12分)
所以直线EC1与底面所成角大小为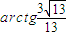 (14分)
(14分)
点评:本题主要考查空间线线、线面、面面关系,二面角、线面角的度量、考查化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.
(2)建立空间直接坐标系,利用平面EFHG法向量与底面法向量夹角去求截面EFGH与底面ABCD所成锐二面角的大小.
(3))因为C1C⊥底面ABCD,所以∠C1EC就是所求的角.在RT△C1CE中 求解即可.
解答:
 解:(1)如图,截面为EFHG
解:(1)如图,截面为EFHG (2)如图,建空间直角坐标系,
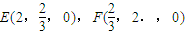 ,
,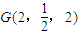 ,
,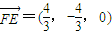 ,
,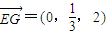 (8分)
(8分)平面EFHG法向量为(-6,-6,1),底面法向量为(0,0,1)
设向量夹角θ,
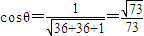 (12分)
(12分)截面EFHG与底面所成锐二面角大小为
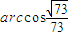 (14分)
(14分)
(3)∵C1C⊥底面ABCD,∴∠C1EC就是所求的角 (9分)
在RT△C1CE中,
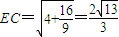 ,
, (12分)
(12分)所以直线EC1与底面所成角大小为
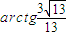 (14分)
(14分)点评:本题主要考查空间线线、线面、面面关系,二面角、线面角的度量、考查化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1= 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.