Question

（本小题满分16分）

某厂生产一种仪器，由于受生产能力和技术水平的限制，会产生一些次品．根据经验知道，该厂生产这种仪器，次品率与日产量（件）之间大体满足关系：

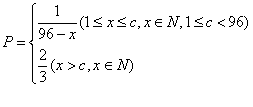
（注：次品率，如表示每生产10件产品，约有1件为次品．其余为合格品．）

已知每生产一件合格的仪器可以盈利元，但每生产一件次品将亏损元，故厂方希望定出合适的日产量，

（1）试将生产这种仪器每天的盈利额（元）表示为日产量（件）的函数；

（2）当日产量为多少时，可获得最大利润？

Answer 1

（1）当时，，所以每天的盈利额． …………………… 2分

       当时，，所以每天生产的合格仪器有件，次品有件，故每天的盈利额，……………4分

       综上，日盈利额（元）与日产量（件）的函数关系为：

． ………………………………………………………6分

       （2）由（1）知，当时，每天的盈利额为0；

当时，，因为， …8分

令，得或,因为＜96，故时，为增函数.

令，得，故时，为减函数.  ……………………………………10分

所以，当时，（等号当且仅当时成立），   ………………………12分

 当时， （等号当且仅当时取得），    ……………14分

       综上，若，则当日产量为84件时，可获得最大利润；若，则当日产量为时，可获得最大利润．………………………………………………………………………………16分