Question

解下列不等式:

(1)|x²-3x-2|≤2;

(2)|x²-2|x|-2|≥1.

Answer 1

解:(1)原不等式化为-2≤x²-3x-2≤2,

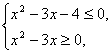    即即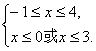

∴-1≤x≤0或3≤x≤4.

    故原不等式的解-1≤x≤0或3≤x≤4.

(2)原不等式化为x²-2|x|-2≥1或x²-2|x|-2≤-1,

    即x²-2|x|-3≥0或x²-2|x|-1≤0,

    即|x|≥3或|x|≤-1(舍)或1-≤|x|≤1+.∴|x|≥3或0≤|x|≤1+.

    故原不等式的解为x≥3或x≤-3或-1-≤x≤1+.