题目内容
已知
，求f（x）的值域．
解：∵，
∴f（2x+1）=
即f（x）=
令f'（x）=
=0
解得x=-2或
当x∈（-∞，-2）时f'（x）=＜0
当x∈（-2，）时f'（x）=＞0
x∈（，+∞）时f'（x）=＜0
∴当x=-2时函数取最小值-1，当x=时函数有最大值4
故函数的值域为[-1，]
分析：先利用配凑法求出函数的解析式，然后求出导函数，求出f′（x）=0的值，再讨论满足f′（x）=0的点附近的导数的符号的变化情况，来确定极值，从而求出函数的值域．
点评：本题主要考查了利用导数研究函数的值域，关于函数的值域的求解最近几年有所弱化，本题属于基础题．
，∴f（2x+1）=
即f（x）=
令f'（x）=
=0解得x=-2或
当x∈（-∞，-2）时f'（x）=
＜0当x∈（-2，
）时f'（x）=＞0x∈（
，+∞）时f'（x）=＜0∴当x=-2时函数取最小值-1，当x=
时函数有最大值4故函数的值域为[-1，
]分析：先利用配凑法求出函数的解析式，然后求出导函数，求出f′（x）=0的值，再讨论满足f′（x）=0的点附近的导数的符号的变化情况，来确定极值，从而求出函数的值域．
点评：本题主要考查了利用导数研究函数的值域，关于函数的值域的求解最近几年有所弱化，本题属于基础题．
练习册系列答案
相关题目
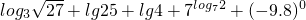
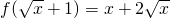，求f（x）的解析式
，求f（x）的解析式
求f（x）的最大值及最小值．
求f（x）的最大值及最小值．
求f（x）的最大值及最小值．