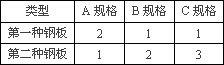
题目内容
设a,b,c均为不等于1的正实数,则下列等式中恒成立的是( )
| A.logab•logcb=logca | B.logab•logaa=logab |
| C.logabc=logab•logac | D.loga(b+c)=logab+logac |
对于A,logab•logcb=logca?logab=
,与换底公式矛盾,所以A不正确;
对于B,logab•logaa=logab,?logab=
,符号换底公式,所以正确;
对于C,logabc=logab•logac,不满足对数运算公式loga(xy)=logax+logay(x、y>0),所以不正确;
对于D,loga(b+c)=logab+logac,不满足loga(xy)=logax+logay(x、y>0),所以不正确;
故选B.
| logca |
| logcb |
对于B,logab•logaa=logab,?logab=
| logcb |
| logca |
对于C,logabc=logab•logac,不满足对数运算公式loga(xy)=logax+logay(x、y>0),所以不正确;
对于D,loga(b+c)=logab+logac,不满足loga(xy)=logax+logay(x、y>0),所以不正确;
故选B.

练习册系列答案
相关题目