题目内容
班主任为了对本班学生的考试成绩进行分析,决定从全班25名女同学,15名男同学中随机抽取一个容量为8的样本进行分析.(I)如果按性别比例分层抽样,男、女生各抽取多少名才符合抽样要求?
(II)随机抽出8名,他们的数学、物理分数对应如下表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
(ii)根据上表数据,用变量y与x的相关系数或散点图说明物理成绩y与数学成绩x之间线性相关关系的强弱.如果有较强的线性相关关系,求y与x的线性回归方程(系数精确到0.01);如果不具有线性相关关系,说明理由.
参考公式:相关系数
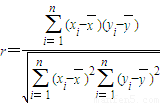 ;
;回归直线的方程是:
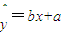 ,其中
,其中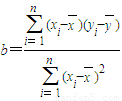 ,
,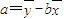 ,
,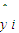 是与xi对应的回归估计值.
是与xi对应的回归估计值.参考数据:
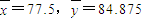 ,
,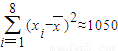 ,
,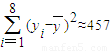 ,
,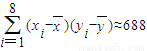 ,
,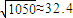 ,
,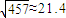 ,
,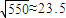 .
.
【答案】分析:(I)从全班25位女同学,15位男同学中随机抽取一个容量为8的样本进行分析,做出女生和男生在总人数中所占的比例,用比例乘以要抽取的样本容量,得到结果.
(II)(i)这是一个古典概率,由表中可以看出,所选的8名同学中,数学和物理分数均为优秀的有3人,根据等可能事件的概率公式得到结果.
(ii)首先求出两个变量的平均数,再利用最小二乘法做出线性回归方程的系数,把做出的系数和x,y的平均数代入公式,求出a的值,写出线性回归方程,得到结果.
解答:解:(Ⅰ)应选女生 名,男生
名,男生 名…(2分)
名…(2分)
(Ⅱ) ( i)由表中可以看出,所选的8名同学中,数学和物理分数均为优秀的有3人,故所求概率是 .…(7分)
.…(7分)
( ii)变量y与x的相关系数是 .
.
可以看出,物理与数学成绩高度正相关.…(10分)
设y与x的线性回归方程是 ,
,
根据所给数据可以计算出 ,a=84.875-0.66×77.5≈33.73,
,a=84.875-0.66×77.5≈33.73,
所以y与x的线性回归方程是 .…(12分)
.…(12分)
点评:本题考查线性回归分析的初步应用,考查分层抽样,考查条件概率,考查相互独立事件同时发生的概率,考查利用数学知识解决实际问题的能力,是一个比较好的综合题目.
(II)(i)这是一个古典概率,由表中可以看出,所选的8名同学中,数学和物理分数均为优秀的有3人,根据等可能事件的概率公式得到结果.
(ii)首先求出两个变量的平均数,再利用最小二乘法做出线性回归方程的系数,把做出的系数和x,y的平均数代入公式,求出a的值,写出线性回归方程,得到结果.
解答:解:(Ⅰ)应选女生
 名,男生
名,男生 名…(2分)
名…(2分)(Ⅱ) ( i)由表中可以看出,所选的8名同学中,数学和物理分数均为优秀的有3人,故所求概率是
 .…(7分)
.…(7分)( ii)变量y与x的相关系数是
 .
.可以看出,物理与数学成绩高度正相关.…(10分)
设y与x的线性回归方程是
 ,
,根据所给数据可以计算出
 ,a=84.875-0.66×77.5≈33.73,
,a=84.875-0.66×77.5≈33.73,所以y与x的线性回归方程是
 .…(12分)
.…(12分)点评:本题考查线性回归分析的初步应用,考查分层抽样,考查条件概率,考查相互独立事件同时发生的概率,考查利用数学知识解决实际问题的能力,是一个比较好的综合题目.

练习册系列答案
相关题目


