题目内容
(本小题16分)
已知等差数列![]() 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列![]() 的首项为b,公比为a,其中a,b都是大于1的正整数,且
的首项为b,公比为a,其中a,b都是大于1的正整数,且![]() .
.
(1)求a的值;
(2)若对于任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求b的值;
成立,求b的值;
(3)令![]() ,问数列
,问数列![]() 中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
解:(1)由已知,得![]() .由
.由![]() ,得
,得![]() .
.
因a,b都为大于1的正整数,故a≥2.又![]() ,故b≥3. …………2分
,故b≥3. …………2分
再由![]() ,得
,得 ![]() .
.
由![]() ,故
,故![]() ,即
,即![]() .
.
由b≥3,故![]() ,解得
,解得![]() . ………………………4分
. ………………………4分
于是![]() ,根据
,根据![]() ,可得
,可得![]() .……………………6分
.……………………6分
(2)由![]() ,对于任意的
,对于任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() ,则
,则
![]() .
.
又![]() ,由数的整除性,得b是5的约数.
,由数的整除性,得b是5的约数.
故![]() ,b=5.
,b=5.
所以b=5时,存在正自然数![]() 满足题意.………………………9分
满足题意.………………………9分
(3)设数列![]() 中,
中,![]() 成等比数列,由
成等比数列,由![]() ,
,![]() ,得
,得
![]() .
.
化简,得![]() . (※) …………………11分
. (※) …………………11分
当![]() 时,
时,![]() 时,等式(※)成立,而
时,等式(※)成立,而![]() ,不成立. ……………12分
,不成立. ……………12分
当![]() 时,
时,![]() 时,等式(※)成立.………………………………………13分
时,等式(※)成立.………………………………………13分
当![]() 时,
时,![]() ,这与b≥3矛盾.
,这与b≥3矛盾.
这时等式(※)不成立.…………………………………………14分
综上所述,当![]() 时,不存在连续三项成等比数列;当
时,不存在连续三项成等比数列;当![]() 时,数列
时,数列![]() 中的第二、三、四项成等比数列,这三项依次是18,30,50.……………………16分
中的第二、三、四项成等比数列,这三项依次是18,30,50.……………………16分

练习册系列答案
相关题目
 轴,焦点
轴,焦点 在直线
在直线 上,直线
上,直线 与抛物线相交于
与抛物线相交于 两点,
两点, 为抛物线上一动点(不同于
为抛物线上一动点(不同于 分别交该抛物线的准线
分别交该抛物线的准线 于点
于点 。
。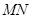 为直径的圆
为直径的圆 经过焦点
经过焦点
 ,
, ,
, , 点P的横坐标为14,且
, 点P的横坐标为14,且 ,点
,点 是边
是边 上一点,且
上一点,且 .
. 的值与点
的值与点 的坐标;
的坐标; 为线段
为线段 上的一个动点,试求
上的一个动点,试求 的取值范围.
的取值范围.