题目内容
甲、乙、丙、丁四人参加某运动会射击项目选拔赛,四人的平均成绩和方差如下表所示:
| | 甲 | 乙 | 丙 | 丁 |
| 平均环数x | 8.3 | 8.8 | 8.8 | 8.7 |
| 方差s2 | 3.5 | 3.6 | 2.2 | 5.4 |
从这四个人中选择一人参加该运动会射击项目比赛,最佳人选是( ).
A.甲 B.乙 C.丙 D.丁
C.
解析试题分析:分析表格可知,乙与丙的平均环数最多,又丙的方差比乙小说明丙成绩发挥的较为稳定,所以最佳人选为丙.
考点:数据的平均数与方差的意义.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
在验证吸烟与否与患肺炎与否有关的统计中,根据计算结果,认为这两件事情无关的可能性不足1%,那么 的一个可能取值为( )
的一个可能取值为( )
| A.6.635 | B.5.024 | C.7.897 | D.3.841 |
某同学使用计算器求30个数据的平均数时,错将其中一个数据105输人为15,那么由此求出的平均数与实际平均数的差是( ).
| A.3.5 | B.-3 | C.3 | D.-0.5 |
为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:
父亲身高 | 174 | 176 | 176 | 176 | 178 |
儿子身高 | 175 | 175 | 176 | 177 | 177 |
则,
 对
对 的线性回归方程为( )
的线性回归方程为( )A.
 B.
B.  C.
C.  D.
D. 
工人工资(元)依劳动生产率(千元)变化的回归方程为y=50+80x,下列判断中正确的是( )
| A.劳动生产率为1000元时,工资为130元 |
| B.劳动生产率平均提高1000元时,工资平均提高80元 |
| C.劳动生产率平均提高1000元时,工资平均提高130元 |
| D.当工资为250元时,劳动生产率为2000元 |
某时段内共有100辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过60km/h的汽车数量为( )
| A.38辆 | B.28辆 | C.10辆 | D.5辆 |
某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
| 学生 | 1号 | 2号 | 3号 | 4号 | 5号 |
| 甲班 | 6 | 7 | 7 | 8 | 7 |
| 乙班 | 6 | 7 | 6 | 7 | 9 |
则以上两组数据的方差中较小的一个为s2,则s2=( )
A.
 B.
B. C.
C. D.2
D.2 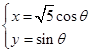 (0≤θ<π)和
(0≤θ<π)和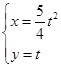 ( t ∈R),求它们的交点坐标.
( t ∈R),求它们的交点坐标.

