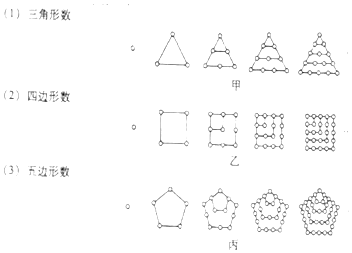
题目内容
15．已知复数z=$\frac{3-4i}{2-i}$，$\overline z$是z的共轭复数，则$|{\overrightarrow{\overline z}}$|为（ ）| A． | $\frac{{5\sqrt{5}}}{3}$ | B． | $\sqrt{5}$ | C． | $\frac{{\sqrt{5}}}{5}$ | D． | $2\sqrt{5}$ |
分析 求出z，$\overline z$，即可得出结论．
解答 解：由z=$\frac{3-4i}{2-i}$=$\frac{（3-4i）（2+i）}{5}$=2-i，∴$\overline z$=2+i，
∴|$\overline z$|=$\sqrt{5}$，
故选B．
点评 本题考查复数的运算，考查学生的计算能力，正确化简是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．已知偶函数y=f（x）对于任意的x∈[0，$\frac{π}{2}$）满足f′（x）cosx+f（x）sinx＞0，（其中f′（x）是函数f（x）的导函数），则下列不等式中成立的是（ ）
| A． | $\sqrt{2}$f（-$\frac{π}{3}$）＜f（$\frac{π}{4}$） | B． | $\sqrt{2}$f（-$\frac{π}{3}$）＜f（-$\frac{π}{4}$） | C． | f（0）$＞\sqrt{2}$f（-$\frac{π}{4}$） | D． | f（$\frac{π}{4}$）$＜\sqrt{3}$f（$\frac{π}{3}$） |
10．设{an}是首项为a1，公比为q的等比数列，则“a1q＞0”是“{an}为递增数列”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
20．集合M={x|x2＜2x}，N={x|log2（x-1）≤0}，则M∩N=（ ）
| A． | （1，2） | B． | （1，2] | C． | [1，2） | D． | （0，2） |
4．若集合M={x∈N|x＜6}，N={x|x2-11x+18＜0}，则M∩N等于（ ）
| A． | {3，4，5} | B． | {x|2＜x＜6} | C． | {x|3≤x≤5} | D． | {2，3，4，5} |
16．
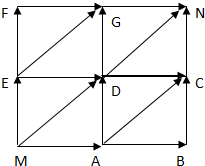某商店老板设计了如下有奖游戏方案：顾客只要花10元钱，即可参加有奖游戏一次．游戏规则如下：棋子从点M开始沿箭头方向跳向N，每次只跳一步（即一个箭头），当下一步有方向选择时，跳的方法必须通过投掷骰子决定，方案如下：当掷出的点数为1时，沿$\overrightarrow{MD}$方向跳一步；当掷出的点数为2，4，6时，沿$\overrightarrow{ME}$方向跳一步；当掷出的点数为3，5时，沿$\overrightarrow{MA}$方向跳一步；奖励标准如表：
若该店平均每天有200人参加游戏，按每月30天计算．则该店开展此游戏每月获利的期望（均值）为2083元
（精确到1元）
某商店老板设计了如下有奖游戏方案：顾客只要花10元钱，即可参加有奖游戏一次．游戏规则如下：棋子从点M开始沿箭头方向跳向N，每次只跳一步（即一个箭头），当下一步有方向选择时，跳的方法必须通过投掷骰子决定，方案如下：当掷出的点数为1时，沿$\overrightarrow{MD}$方向跳一步；当掷出的点数为2，4，6时，沿$\overrightarrow{ME}$方向跳一步；当掷出的点数为3，5时，沿$\overrightarrow{MA}$方向跳一步；奖励标准如表：| 从M到N用的步数 | 2 | 3 | 4 |
| 奖励金额（元） | 100 | 10 | 5 |
（精确到1元）