题目内容
已知向量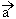 =(
=(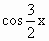 ,
,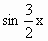 ),
),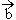 =(
=(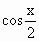 ,-
,-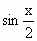 ),且x∈[0,
),且x∈[0,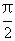 ],求
],求
(1)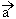 ·
·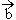 及|
及|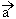 +
+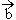 |;
|;
(2)若f(x)=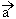 ·
·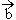 -2λ|
-2λ|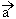 +
+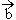 |的最小值是-
|的最小值是-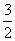 ,求λ的值.
,求λ的值.
答案:
解析:
解析:
|
解:(1) | = ∵x∈[0, (2)f(x)=cos2x-4λcosx,即f(x)=2(cosx-λ)2-1-2λ2 ∵x∈[0, ①当λ<0时,当且仅当cosx=0时,f(x)取得最小值-1,这与已知矛盾; ②当0≤λ≤1时,当且仅当cosx=λ时,f(x)取得最小值-1-2λ2,由已知得-1-2λ2=- ③当λ>1时,当且仅当cosx=1时,f(x)取得最小值1-4λ.由已知得1-4λ=- 解得λ= |

练习册系列答案
相关题目
 ·
· =
= ·
· -
- ·
· =cos2x
=cos2x
 =
=
 ],∴cosx>0,∴|
],∴cosx>0,∴| ,解得λ=
,解得λ= ;
; ,这与λ>1相矛盾.综上所述,λ=
,这与λ>1相矛盾.综上所述,λ= 为所求.
为所求. (a、b、c∈N),f(2)=2,f(3)<3且f(x)的图像按向量e=(-1,0)平移后得到的图像关于原点对称.
(a、b、c∈N),f(2)=2,f(3)<3且f(x)的图像按向量e=(-1,0)平移后得到的图像关于原点对称.