题目内容
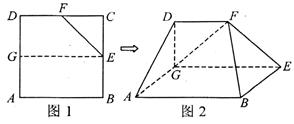
(本小题满分12分)如图:直角梯形ABCD中,AD∥BC,∠ABC=90°,E、F分别是边AD和BC上的点,且EF∥AB,AD ="2AE" ="2AB" =" 4AF=" 4,将四边形EFCD沿EF折起使AE=AD.
(1)求证:AF∥平面CBD;
(2)求平面CBD与平面ABFE夹角的余弦值.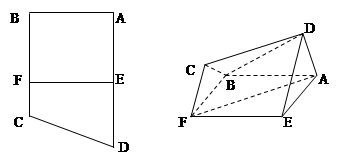
(1)求证:AF∥平面CBD;
(2)求平面CBD与平面ABFE夹角的余弦值.
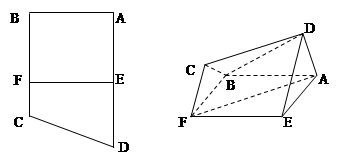
(1)见解析 (2)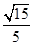
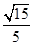
(1)利用直线与平面平行的判定证明线面平行;(2)根据条件建立空间直角坐标系,然后求出两个面的法向量,根据法向量的夹角求出二面角
(1)证明: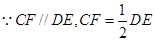 ,所以延长
,所以延长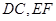 会相交,
会相交,
设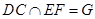 ,则
,则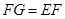 ,
,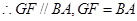 ,
,
所以四边形 是平行四边形,
是平行四边形,
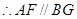 ,又
,又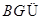 平面
平面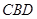
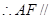 平面
平面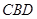 ;……………………6分
;……………………6分
(2)设 的中点为
的中点为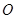 ,
,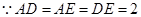 ,则
,则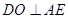 且
且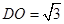 ,
,
又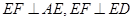 ,
,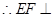 平面
平面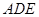 ,
,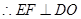 ,
,
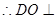 平面
平面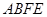 .………………………………………………………………8分
.………………………………………………………………8分
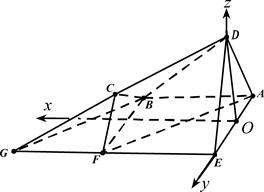
如图:以点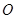 为原点,过点
为原点,过点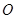 且平行于
且平行于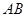 的直线为
的直线为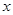 轴,
轴, 所在直线为
所在直线为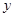 轴,
轴,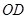 所在直线为
所在直线为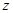 轴,建立空间直角坐标系
轴,建立空间直角坐标系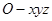 。则平面
。则平面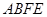 的法向量为
的法向量为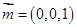 ,点
,点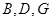 的坐标分别为
的坐标分别为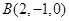 ,
,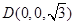 ,
,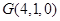 ,………………10分
,………………10分
设平面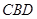 的法向量
的法向量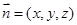 ,则
,则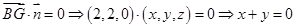 ,
,
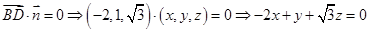
令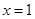 ,则
,则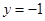 ,
,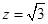 ,即
,即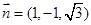 ,
,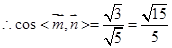 ,
,
平面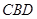 与平面
与平面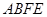 夹角的余弦值为
夹角的余弦值为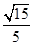 .…………………………………12分
.…………………………………12分
(1)证明:
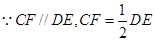 ,所以延长
,所以延长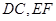 会相交,
会相交,设
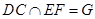 ,则
,则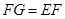 ,
,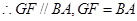 ,
,所以四边形
 是平行四边形,
是平行四边形,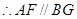 ,又
,又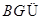 平面
平面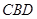
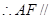 平面
平面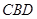 ;……………………6分
;……………………6分(2)设
 的中点为
的中点为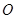 ,
,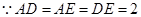 ,则
,则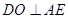 且
且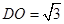 ,
,又
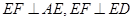 ,
,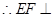 平面
平面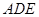 ,
,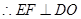 ,
,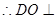 平面
平面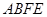 .………………………………………………………………8分
.………………………………………………………………8分如图:以点
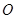 为原点,过点
为原点,过点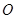 且平行于
且平行于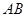 的直线为
的直线为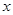 轴,
轴, 所在直线为
所在直线为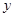 轴,
轴,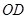 所在直线为
所在直线为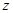 轴,建立空间直角坐标系
轴,建立空间直角坐标系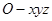 。则平面
。则平面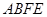 的法向量为
的法向量为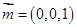 ,点
,点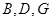 的坐标分别为
的坐标分别为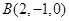 ,
,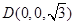 ,
,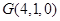 ,………………10分
,………………10分
设平面
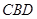 的法向量
的法向量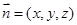 ,则
,则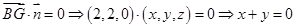 ,
,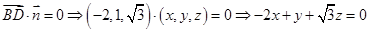
令
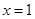 ,则
,则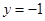 ,
,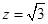 ,即
,即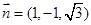 ,
,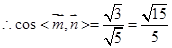 ,
,平面
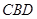 与平面
与平面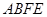 夹角的余弦值为
夹角的余弦值为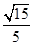 .…………………………………12分
.…………………………………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
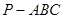 中,
中,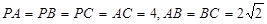
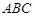 ⊥平面
⊥平面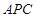
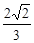 ,求BM的最小值.
,求BM的最小值.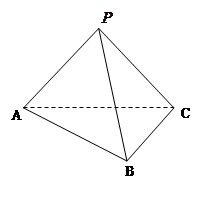
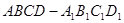 中,
中,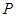 为正方形
为正方形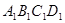 四边上的动点,
四边上的动点,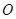 为底面正方形
为底面正方形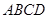 的中心,
的中心,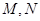 分别为
分别为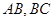 的中点,点
的中点,点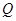 为平面
为平面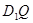 与
与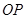 互相平分,则满足
互相平分,则满足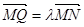 的实数
的实数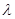 的值有( )
的值有( )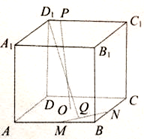
 个
个 个
个 个
个 个
个 的所有顶点都在球
的所有顶点都在球 的求面上,
的求面上, 是边长为
是边长为 的正三角形,
的正三角形, 为球
为球 ;则此棱锥的体积为( )
;则此棱锥的体积为( )



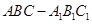 中,底面
中,底面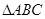 为等腰直角三角形,
为等腰直角三角形,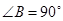 ,
,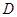 为棱
为棱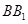 上一点,且平面
上一点,且平面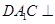 平面
平面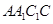 .
.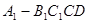 和
和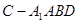 的体积是否相等,并证明。
的体积是否相等,并证明。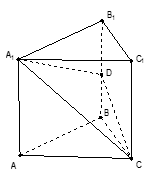
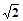 ,求AB1与C1B所成角的大小。
,求AB1与C1B所成角的大小。