题目内容
某单位有员工1000名,平均每人每年创造利润10万元。为了增加企业竞争力,决定优化产业结构,调整出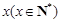 名员工从事第三产业,调整后他们平均每人每年创造利为
名员工从事第三产业,调整后他们平均每人每年创造利为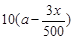 万元
万元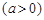 ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高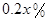 .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)在(1)的条件下,若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则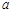 的取值范围是多少?
的取值范围是多少?
(1)500(2)
解析试题分析:(1)由题意找出关于x的不等式:
解不等式可求得最多调整出多少名员工从事第三产业.
(2)从事第三产业的员工创造的年总利润为 万元,从事原来产业的员工的年总利润为
万元,从事原来产业的员工的年总利润为
 万元,找出关于x的不等式:
万元,找出关于x的不等式: 恒成立,
恒成立,
用分离参数法得
 恒成立,从而转化为关于x的函数求最值,由均值不等式得
恒成立,从而转化为关于x的函数求最值,由均值不等式得
试题解析:解:(1)由题意得:
即 又
又 所以
所以
即最多调整500名员工从事第三产业.
(2)从事第三产业的员工创造的年总利润为 万元,从事原来产业的员工的年总利润为
万元,从事原来产业的员工的年总利润为
 万元,
万元,
则 恒成立,
恒成立,
所以
 , 所以
, 所以

 ,
,
即
 恒成立,
恒成立,
因为
 ,
,
当且仅当 ,即
,即 时等号成立.
时等号成立.
所以 ,又
,又 ,所以
,所以 ,
,
即 的取值范围为
的取值范围为 .
.
考点:利用不等式求最值

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
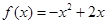 .
.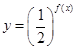 的最小值;
的最小值;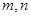 ,当
,当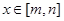 时,
时,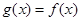 ,且
,且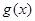 的值域为
的值域为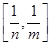 ?若存在,求出所有的
?若存在,求出所有的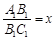 ,求公园ABCD所占面积S关于x的函数解析式;
,求公园ABCD所占面积S关于x的函数解析式;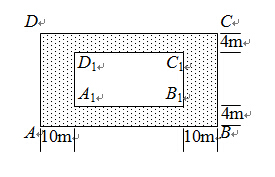
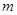 (单位:万元)的关系有经验公式
(单位:万元)的关系有经验公式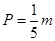 ,
, 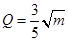 . 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资
. 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资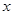 (单位:万元)
(单位:万元)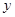 (单位:万元)关于
(单位:万元)关于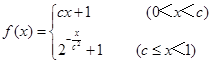 ,且
,且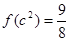 .
.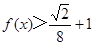 .
.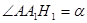 .
.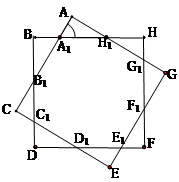
 表示
表示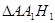 的面积;
的面积;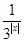 .
.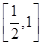 恒成立,求m的取值范围.
恒成立,求m的取值范围. 的值域为________________________.
的值域为________________________.