题目内容
已知 分另为椭圆的上、下焦点,
分另为椭圆的上、下焦点, 是抛物线
是抛物线 的焦点,点
的焦点,点 是
是 与
与 在第二象限的交点, 且
在第二象限的交点, 且
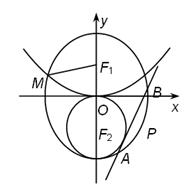
(1)求椭圆 的方程;
的方程;
(2)与圆 相切的直线
相切的直线 交椭圆
交椭圆 于
于 ,若椭圆
,若椭圆 上一点
上一点 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围.
(Ⅰ)由题知 ,所以
,所以 , 又由抛物线定义可知
, 又由抛物线定义可知 ,得
,得 ,于是易知
,于是易知 ,从而
,从而 ,由椭圆定义知
,由椭圆定义知 ,得
,得 ,故
,故 ,从而椭圆的方程为
,从而椭圆的方程为
 分
分
(Ⅱ)设 ,则由
,则由 知,
知,
 ,且
,且 , ①
, ①
又直线 与圆
与圆 相切,所以有
相切,所以有 ,
,
由 ,可得
,可得 ②
②
又联立 消去
消去 得
得
且 恒成立,且
恒成立,且 ,
,
所以 ,所以得
,所以得
 分
分
代入①式得 ,所以
,所以
又将②式代入得, ,
,  分
分
易知 ,所以
,所以 ,
,
所以 的取值范围为
的取值范围为
 分
分
考点:抛物线的性质,椭圆的定义,直线与圆的位置关系,直线与椭圆的位置关系,向量的关系,函数值域问题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 在
在 上是单调函数,则实数
上是单调函数,则实数 的取值范围是( )
的取值范围是( ) B.
B.  C.
C.  D.
D.
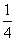 AB,且对于边AB上任一点P,恒有
AB,且对于边AB上任一点P,恒有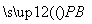 ·
·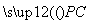 ≥
≥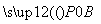 ·
·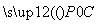 ,则( )
,则( ) 在区间(-∞,2
在区间(-∞,2 上是减函数,则实数
上是减函数,则实数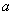 的取值范围是( )
的取值范围是( ) -
- ,+∞) B.(-∞,-
,+∞) B.(-∞,- :
: ,条件
,条件 :
: ,则
,则 是
是 的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为 ( )
的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为 ( ) D.
D.
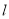 经过点
经过点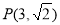 ,且与
,且与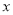 轴交于点F(2,0)。
轴交于点F(2,0)。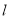 的方程;
的方程; 中,角
中,角 所对的边分别是
所对的边分别是 ,若
,若 ,且
,且 .
. 的值;
的值; ,求
,求 的面积.
的面积.