题目内容
（（本题14分）如图3，四棱锥P—ABCD中，底面ABCD是矩形，PA⊥平面ABCD，M、N分别是AB、PC的中点，PA=AD=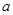
。
(Ⅰ)求证：MN//平面PAD；
(Ⅱ)求证：平面PMC⊥平面PCD；
(Ⅲ)若二面角P—MC—A是60°的二面角，求四棱锥P—ABCD的体积。
证明：(Ⅰ)如答图所示，⑴设PD的中点为E，连结AE、NE，
由N为PD的中点知EN
DC，
又ABCD是矩形，∴DCAB，∴ENAB
又M是AB的中点，∴ENAN，
…3分
∴AMNE是平行四边形
∴MN∥AE，而AE
平面PAD，NM
平面PAD
∴MN∥平面PAD …4分
(Ⅱ)∵PA＝AD，∴AE⊥PD，
又∵PA⊥平面ABCD，CD平面ABCD，
∴CD⊥PA，而CD⊥AD，∴CD⊥平面PAD …6分
∴CD⊥AE， ∵PD∩CD＝D，∴AE⊥平面PCD，
∵MN∥AE，∴MN⊥平面PCD，又MN平面PMC，
∴平面PMC⊥平面PCD. …8分
（Ⅲ）解：过A作AH⊥CM，交CM的延长线于H，连PH．
∵PA⊥平面ABCD，AH⊥CH，∴PH⊥CH， ∴∠PHA是二面角P－MC－A的平面角，
∴AH＝
… 10分
又∵Rt△MHA∽Rt△MBC，
∴
…12分
∴
…
14分
解法二：(Ⅱ)以A为原点，AB,AD,AP所在直线分别为
轴、
轴、
轴建系
设AB=b
(b>0) 面PMC法向量
面PDC法向量
∵
∴面PMC
面PDC
…8分
（Ⅲ）面MCA法向量
∵二面角P—MC—A是60°的二面角
∴
∴
…12分
∴
…14分
【解析】略
和梯形
所在平面互相垂直，
，
，
，
．
平面
；
的长为何值时，二面角
的大小为
？
如图，
分别是正方体
的
的中点．
//平面
；
平面
中,底面ABCD是矩形，PA⊥平面ABCD，PA=AB=1，BC=2，E为PD
的中点
中,底面ABCD是矩形，PA⊥平面ABCD，PA=AB=1，BC=2，E为PD的中点