题目内容
过点P(2,3)的直线l被两平行直线l1:2x-5y+9=0与l2:2x-5y-7=0所截线段AB的中点恰在直线x-4y-1=0上.(Ⅰ)求l1和l2间的距离;
(Ⅱ)求直线l的方程.
【答案】分析:(I)由两条平行线之间的距离公式,结合题中数据加以计算即可得到l1和l2间的距离;
(II)求出位于直线l1和l2之间,且与直线l1和l2距离相等的直线方程,与直线x-4y-1=0联解得到AB中点坐标为C(-3,-1),从而求出直线PC方程,即得所求直线l的方程.
解答:解:(I)根据两条平行线之间的距离公式,得
l1和l2间的距离d=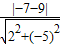 =
=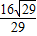 ;
;
(II)由题意,AB的中点必定在直线2x-5y+1=0上,
联解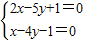 ,得中点坐标为C(-3,-1)
,得中点坐标为C(-3,-1)
∵点P坐标为(2,3),
∴PC的斜率为k=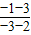 =
= ,得直线PC的方程为y-3=
,得直线PC的方程为y-3= (x-2)
(x-2)
化简,得y= x+
x+ ,即为所求直线l的方程.
,即为所求直线l的方程.
点评:本题给出平行直线,求经过定点且被平行直线截得中点在定直线上的直线方程.着重考查了直线的基本量与基本形式、直线的位置关系和距离公式等知识,属于中档题.
(II)求出位于直线l1和l2之间,且与直线l1和l2距离相等的直线方程,与直线x-4y-1=0联解得到AB中点坐标为C(-3,-1),从而求出直线PC方程,即得所求直线l的方程.
解答:解:(I)根据两条平行线之间的距离公式,得
l1和l2间的距离d=
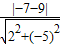 =
=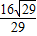 ;
;(II)由题意,AB的中点必定在直线2x-5y+1=0上,
联解
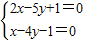 ,得中点坐标为C(-3,-1)
,得中点坐标为C(-3,-1)∵点P坐标为(2,3),
∴PC的斜率为k=
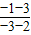 =
= ,得直线PC的方程为y-3=
,得直线PC的方程为y-3= (x-2)
(x-2)化简,得y=
 x+
x+ ,即为所求直线l的方程.
,即为所求直线l的方程.点评:本题给出平行直线,求经过定点且被平行直线截得中点在定直线上的直线方程.着重考查了直线的基本量与基本形式、直线的位置关系和距离公式等知识,属于中档题.

练习册系列答案
相关题目
 的离心率为
的离心率为 ,直线
,直线 :
: 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切. ,右焦点
,右焦点 ,直线
,直线 过点
过点 垂
垂 ,线段
,线段 垂直平分线交
垂直平分线交 ,求点
,求点 的方程;
的方程; 轴上时,在曲线
轴上时,在曲线 过点A(a,0),B(0,b)的直
过点A(a,0),B(0,b)的直 ,原点到该直线的距离为
,原点到该直线的距离为 .
. 求直线MN的方程;
求直线MN的方程; 交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。 +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).