题目内容
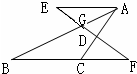如图，在△ABC中，D为AC边上的中点，AE∥BC，ED交AB于点G，交BC延长线于点F，若BG：GA=3：1，BC=10，则AE的长为5
5
．分析：可证得△ADE≌△CDF，则AE=CF，又△AEG∽△BFG，则BG：GA=AE：BF，可得出CF：BF=3：1，根据BC=10，求AE的长即可．
解答：解：∵AE∥BC，
∴∠E=∠F，
∵∠ADE=∠CDF，AD=CD，
∴△ADE≌△CDF，
∴AE=CF，
∵AE∥BC，
∴△AEG∽△BFG，
∴
=
，
∵
=
，
∴
=
，
∴
=
，
∴
=
，
∵BC=10，
∴CF=5，
即AE=5．
故答案为：5．
∴∠E=∠F，
∵∠ADE=∠CDF，AD=CD，
∴△ADE≌△CDF，
∴AE=CF，
∵AE∥BC，
∴△AEG∽△BFG，
∴
| BG |
| AG |
| BF |
| AE |
∵
| BG |
| AG |
| 3 |
| 1 |
∴
| BF |
| AE |
| 3 |
| 1 |
∴
| BF |
| CF |
| 3 |
| 1 |
∴
| BC |
| CF |
| 2 |
| 1 |
∵BC=10，
∴CF=5，
即AE=5．
故答案为：5．
点评：本题考查了相似三角形的判定和性质以及平行线分线段成比例的性质问题，应熟练掌握．
练习册系列答案
相关题目
如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在△ABC中，设
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
如图，在△ABC中，已知