题目内容
若直线ax+by=1(ab≠0)与圆x2+y2=1有公共点,则( )A.a2+b2≤1
B.a2+b2≥1
C.
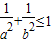
D.
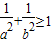
【答案】分析:根据直线ax+by=1和圆x2+y2=1有公共点,通过圆心到直线的距离小于等于半径,即可推出a,b关系.
解答:解:因为直线ax+by=1和圆x2+y2=1有公共点,
所以圆心到直线ax+by-1=0的距离d=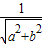 ≤1,
≤1,
解得a2+b2≥1,
故选B.
点评:本题主要考查了直线与圆的位置关系,考查计算能力.
解答:解:因为直线ax+by=1和圆x2+y2=1有公共点,
所以圆心到直线ax+by-1=0的距离d=
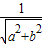 ≤1,
≤1,解得a2+b2≥1,
故选B.
点评:本题主要考查了直线与圆的位置关系,考查计算能力.

练习册系列答案
相关题目
若直线ax+by+1=0(a、b>0)过圆x2+y2+8x+2y+1=0的圆心,则
+
的最小值为( )
| 1 |
| a |
| 4 |
| b |
| A、8 | B、12 | C、16 | D、20 |