题目内容
请设计一个同时满足下列两个条件的函数y=f(x):
(1)图象关于y轴对称;
(2)对定义域内任意不同两点x1,x2,都有 .
.
答案:______.
解:∵图象关于y轴对称,∴此函数为偶函数,∵对定义域内任意不同两点x1,x2,都有 ,
,
∴此函数的图象是向上凸起的,
进而结合函数的性质,
可得答案是 y=cosx,x∈[- ,
, ].
].
注意此题的答案不唯一,如y=-2x2等都可以.
分析:由条件判断函数是偶函数,图象是向上凸起的,进而结合函数的性质,可得答案,注意答案不唯一,满足这两点即可.
点评:本题考查抽象函数的图象特征,答案不唯一,也可以是 y=-x2等.
 ,
,∴此函数的图象是向上凸起的,
进而结合函数的性质,
可得答案是 y=cosx,x∈[-
 ,
, ].
].注意此题的答案不唯一,如y=-2x2等都可以.
分析:由条件判断函数是偶函数,图象是向上凸起的,进而结合函数的性质,可得答案,注意答案不唯一,满足这两点即可.
点评:本题考查抽象函数的图象特征,答案不唯一,也可以是 y=-x2等.

练习册系列答案
相关题目
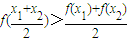 .
.