Question

（1）用反证法证明：在一个三角形中，至少有一个内角大于或等于60°.
（2）已知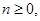试用分析法证明： .

Answer 1

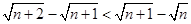（1）先假设再根据三角形内角和定理即可得出矛盾.
（2）按照分析法的一般步骤由要证结论出发，得出1>0，即得证.

解析试题分析：（1）证明：假设在一个三角形中，没有一个内角大于或等于60°，
即均小于60°，
则三内角和小于180°，与三角形中三内角和等于180°矛盾，故假设不成立 .原命题成立 .
（2）证明：要证上式成立，需证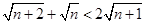    
需证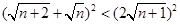          
需证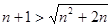                   
需证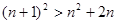    
需证，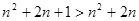            
只需证1>0                               
因为1>0显然成立，所以原命题成立 .  
考点：反证法．
点评：反证法的步骤是：（1）假设结论不成立；（2）从假设出发推出矛盾；（3）假设不成立，则结论成立．在假设结论不成立时，要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．