题目内容
 (2013•朝阳区二模)某三棱锥的三视图如图所示,则该三棱锥的体积为( )
(2013•朝阳区二模)某三棱锥的三视图如图所示,则该三棱锥的体积为( )分析:由三视图及题设条件知,此几何体为一个三棱锥,其高为1,底面是直角边长度为1的等腰直角三角形,故先求出底面积,再由体积公式求解其体积即可.
解答: 解:由题设条件,此几何几何体为一个三棱锥,
解:由题设条件,此几何几何体为一个三棱锥,
如图红色的部分.
其高已知为1,底面是直角边长度为1的等腰直角三角形,
底面积是
×1×1=
其体积是
×
×1=
.
故选A.
 解:由题设条件,此几何几何体为一个三棱锥,
解:由题设条件,此几何几何体为一个三棱锥,如图红色的部分.
其高已知为1,底面是直角边长度为1的等腰直角三角形,
底面积是
| 1 |
| 2 |
| 1 |
| 2 |
其体积是
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
故选A.
点评:本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是.三视图的投影规则是:“主视、俯视 长对正;主视、左视高平齐,左视、俯视 宽相等”.三视图是新课标的新增内容,在以后的高考中有加强的可能.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
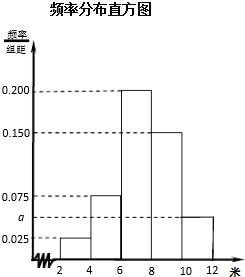 (2013•朝阳区二模)为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成[2,4),[4,6),[6,8),[8,10),[10,12]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
(2013•朝阳区二模)为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成[2,4),[4,6),[6,8),[8,10),[10,12]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.