题目内容
(本题共10分)已知函数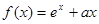 。
。
(Ⅰ)若曲线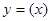 在
在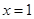 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值;
(Ⅱ)若函数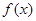 在区间(
在区间(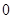 ,
,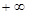 )内是增函数,求
)内是增函数,求 的取值范围。
的取值范围。
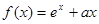 。
。(Ⅰ)若曲线
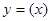 在
在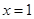 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值;(Ⅱ)若函数
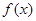 在区间(
在区间(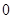 ,
,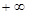 )内是增函数,求
)内是增函数,求 的取值范围。
的取值范围。(1)
(2)

(2)

本试题主要是考查而来导数在研究函数中的运用,求解函数在某点的切线方程,以及函数的单调区间,求解参数的范围的综合运用。逆向求解是解决该题的难点。
(1)求解导数,然后得到曲线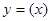 在
在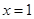 处的导数值,即为切线的斜率,然后利用点斜式得到结论。
处的导数值,即为切线的斜率,然后利用点斜式得到结论。
(2)因为函数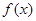 在区间(
在区间(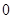 ,
,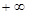 )内是增函数,则导数恒大于等于零,得到参数a的范围。
)内是增函数,则导数恒大于等于零,得到参数a的范围。
解:(1) ………………………… 5分
………………………… 5分
(2) ………………………… 10分
………………………… 10分
(1)求解导数,然后得到曲线
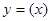 在
在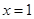 处的导数值,即为切线的斜率,然后利用点斜式得到结论。
处的导数值,即为切线的斜率,然后利用点斜式得到结论。(2)因为函数
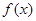 在区间(
在区间(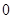 ,
,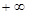 )内是增函数,则导数恒大于等于零,得到参数a的范围。
)内是增函数,则导数恒大于等于零,得到参数a的范围。解:(1)
 ………………………… 5分
………………………… 5分(2)
 ………………………… 10分
………………………… 10分
练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
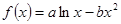 图象上一点P(2,f(2))处的切线方程为
图象上一点P(2,f(2))处的切线方程为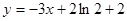 .
.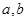 的值;
的值;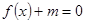 在
在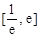 内有两个不等实根,求
内有两个不等实根,求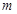 的取值范围(其中
的取值范围(其中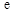 为自然对数的底);
为自然对数的底);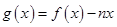 ,如果
,如果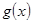 图象与
图象与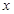 轴交于
轴交于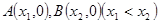 ,AB中点为
,AB中点为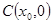 ,求证:
,求证: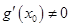 .
.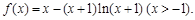
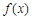 的单调区间;
的单调区间;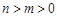 时,
时,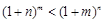 ;
;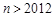 ,且
,且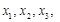 …,
…,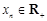 ,
,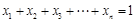 时,
时,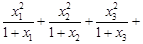 …
…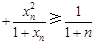
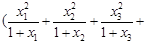 …
…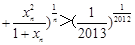 .
.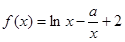 。
。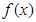 的单调区间;
的单调区间;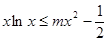 在
在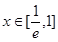 上恒成立,求
上恒成立,求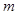 的取值范围。
的取值范围。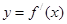 的图象,那么函数
的图象,那么函数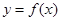 在下面哪个区间是减函数( )
在下面哪个区间是减函数( )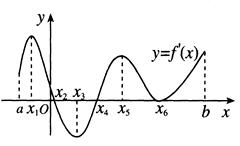
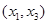

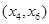
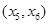
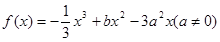 在
在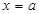 处取得极值.
处取得极值.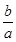 ;
;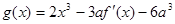 ,如果
,如果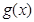 在开区间
在开区间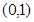 上存在极小值,求实数
上存在极小值,求实数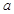 的取值范围.
的取值范围.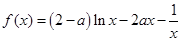 .
.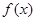 的单调性;
的单调性;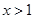 时,
时,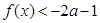 ,求实数
,求实数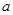 的取值范围;
的取值范围;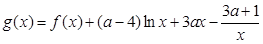 ,若
,若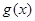 在区间
在区间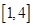 上不单调, 求实数
上不单调, 求实数