题目内容
已知二次函数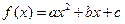 对于
对于 1、
1、 2
2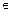 R,且
R,且 1<
1< 2时
2时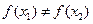 ,求证:方程
,求证:方程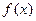 =
=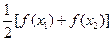 有不等实根,且必有一根属于区间(
有不等实根,且必有一根属于区间( 1,
1, 2).
2).
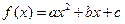 对于
对于 1、
1、 2
2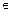 R,且
R,且 1<
1< 2时
2时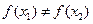 ,求证:方程
,求证:方程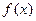 =
=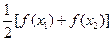 有不等实根,且必有一根属于区间(
有不等实根,且必有一根属于区间( 1,
1, 2).
2).见解析
设F( )=
)=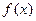 -
-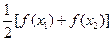 ,
,
则方程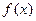 =
=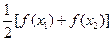 ①
①
与方程 F( )=0 ② 等价
)=0 ② 等价
∵F( 1)=
1)=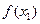 -
-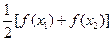 =
=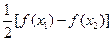
F( 2)=
2)=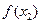 -
-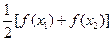 =
=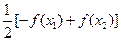
∴ F( 1)·F(
1)·F( 2)=-
2)=-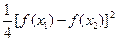 ,又
,又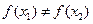
∴F( 1)·F(
1)·F( 2)<0
2)<0
故方程②必有一根在区间( 1,
1, 2)内.由于抛物线y=F(
2)内.由于抛物线y=F( )在
)在 轴上、下方均有分布,所以此抛物线与
轴上、下方均有分布,所以此抛物线与 轴相交于两个不同的交点,即方程②有两个不等的实根,从而方程①有两个不等的实根,且必有一根属于区间(
轴相交于两个不同的交点,即方程②有两个不等的实根,从而方程①有两个不等的实根,且必有一根属于区间( 1,
1, 2).
2).
 )=
)=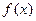 -
-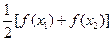 ,
, 则方程
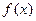 =
=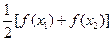 ①
①与方程 F(
 )=0 ② 等价
)=0 ② 等价∵F(
 1)=
1)=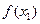 -
-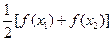 =
=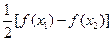
F(
 2)=
2)=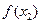 -
-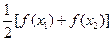 =
=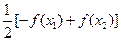
∴ F(
 1)·F(
1)·F( 2)=-
2)=-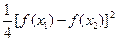 ,又
,又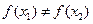
∴F(
 1)·F(
1)·F( 2)<0
2)<0故方程②必有一根在区间(
 1,
1, 2)内.由于抛物线y=F(
2)内.由于抛物线y=F( )在
)在 轴上、下方均有分布,所以此抛物线与
轴上、下方均有分布,所以此抛物线与 轴相交于两个不同的交点,即方程②有两个不等的实根,从而方程①有两个不等的实根,且必有一根属于区间(
轴相交于两个不同的交点,即方程②有两个不等的实根,从而方程①有两个不等的实根,且必有一根属于区间( 1,
1, 2).
2).
练习册系列答案
相关题目
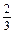 .
.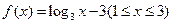 ,设
,设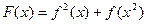

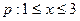 ,条件
,条件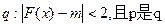 的充分条件,求实数m的取值范围.
的充分条件,求实数m的取值范围. 

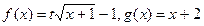 ,(
,(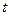 为参数) (1)当
为参数) (1)当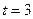 时,解不等式
时,解不等式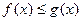 (2)如果当
(2)如果当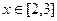 时,
时,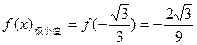
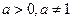 ,函数
,函数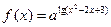 有最大值,则不等式
有最大值,则不等式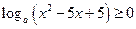
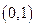 上是增函数的是( )
上是增函数的是( )



 ,且函数
,且函数 有最小值
有最小值 ,则
,则 =__________。
=__________。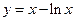 的增区间为( )
的增区间为( )