��Ŀ����
11��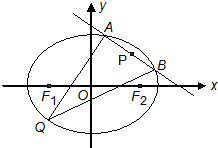 ��ͼ��ʾ����֪��ԲC�ķ���Ϊ$\frac{x^2}{2}+{y^2}$=1��F1��F2�ֱ�����ԲC�����ҽ��㣬ֱ��AB��y=kx+m��k��0������ԲC���ڲ�ͬ��A��B���㣮
��ͼ��ʾ����֪��ԲC�ķ���Ϊ$\frac{x^2}{2}+{y^2}$=1��F1��F2�ֱ�����ԲC�����ҽ��㣬ֱ��AB��y=kx+m��k��0������ԲC���ڲ�ͬ��A��B���㣮���� ��k=-1��m=$\sqrt{2}$����P��ֱ��AB����|PF1|+|PF2|����Сֵ��
���� �����߶�ABΪֱ����Բ������F2����ԭ��O��ֱ��AB�ľ���Ϊ$\frac{{2\sqrt{5}}}{5}$��
��1����ֱ��AB�ķ��̣�
��2������ԲC�����Q�����꣬ʹ�á�ABQ��������
���� ���������Բ�Ľ������ֱ꣬��AB�ķ��̣����F2����ֱ��AB�ĶԳ�${F}_{2}�䣨\sqrt{2}��\sqrt{2}-1��$��Ȼ�����|PF1|+|PF2|����Сֵ��
����1�����A��B������ֱ�ΪA��x1��y1����B��x2��y2��������ԭ��O��ֱ��AB�ľ���õ�m��k�Ĺ�ϵ������y=kx+m��$\frac{x^2}{2}+{y^2}=1$��ͨ��Τ�ﶨ���Լ�$\overrightarrow{A{F_2}}•\overrightarrow{B{F_2}}=0$�����m��k��ֵ��Ȼ�����AB�ķ��̣�
��2���ɣ�1����֪��|AB|�Ƕ�ֵ������ԲC�ϵĵ�Qʹ�á�ABQ��������ʱ����Q��ֱ��AB�ľ���Ϊ�����QΪ��ֱ��AB���·�ƽ����AB������ԲC���е��е㣮��ƽ����AB������ԲC���е����߷��̣�����Բ�����������б�ʽΪ0����⼴�ɣ�
��� �⣺���� ����Բ���̿ɵã���������ΪF1��-1��0����F2��1��0���� ����1�֣�
��k=-1��$m=\sqrt{2}$ʱ��ֱ��AB�ķ���Ϊ$y=-x+\sqrt{2}$�� ����2�֣�
��ɵ�F2��1��0������ֱ��AB�ĶԳƵ�Ϊ${F}_{2}�䣨\sqrt{2}��\sqrt{2}-1��$�� ����3�֣�
��|PF1|+|PF2|����СֵΪ��$|{F}_{1}{F}_{2}��|=\sqrt{{��\sqrt{2}+1��}^{2}+{��\sqrt{2}-1��}^{2}}=\sqrt{6}$�� ����4�֣�
������1�����A��B������ֱ�ΪA��x1��y1����B��x2��y2����
��ԭ��O��ֱ��AB�ľ���Ϊ$\frac{{2\sqrt{5}}}{5}$����$\frac{|m|}{{\sqrt{1+{k^2}}}}=\frac{{2\sqrt{5}}}{5}$����${m^2}=\frac{4}{5}��1+{k^2}��$���١���5�֣�
��y=kx+m����$\frac{x^2}{2}+{y^2}=1$���ã�1+2k2��x2+4kmx+2m2-2=0��
���=16k2m2-4��1+2k2����2m2-2��=8��2k2-m2+1����0����${x_1}+{x_2}=-\frac{4km}{{1+2{k^2}}}��{x_1}{x_2}=\frac{{2{m^2}-2}}{{1+2{k^2}}}$�� ����6�֣�
����֪����$\overrightarrow{A{F_2}}•\overrightarrow{B{F_2}}=0$������x1-1����x2-1��+y1y2=0�� ����7�֣�
�ࣨx1-1����x2-1��+��kx1+m����kx2+m��=0��
��$��1+{k^2}��{x_1}{x_2}+��km-1����{x_1}+{x_2}��+{m^2}+1=0$��
��$��1+{k^2}��•\frac{{2{m^2}-2}}{{1+2{k^2}}}+��km-1��•\frac{-4km}{{1+2{k^2}}}+{m^2}+1=0$��
����3m2+4km-1=0���ڡ���8�֣�
�ɢ٢ڣ���${m^2}=\frac{4}{5}[1+{��\frac{{1-3{m^2}}}{4m}��^2}]$����11m4-10m2-1=0����m2=1��
��k��0����$\left\{\begin{array}{l}m=1\\ k=-\frac{1}{2}\end{array}\right.$�������=8��2k2-m2+1����0��
��AB�ķ���Ϊ$y=-\frac{1}{2}x+1$�� ����9�֣�
��2���ɣ�1����֪��|AB|�Ƕ�ֵ������ԲC�ϵĵ�Qʹ�á�ABQ��������ʱ����Q��ֱ��AB�ľ���Ϊ�����QΪ��ֱ��AB���·�ƽ����AB������ԲC���е��е㣮��ƽ����AB������ԲC���е����߷���Ϊ$y=-\frac{1}{2}x+n��n��0��$����$\left\{\begin{array}{l}y=-\frac{1}{2}x+n\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$��$\frac{3}{2}{x^2}-2nx+2{n^2}-2=0$�����=-8n2+12=0��
��$n=-\frac{{\sqrt{6}}}{2}$����$n=\frac{{\sqrt{6}}}{2}$��ȥ��������11�֣�
�Ӷ����ɵ�Q������Ϊ$Q��-\frac{{\sqrt{6}}}{3}��-\frac{{\sqrt{6}}}{3}��$�� ����12�֣�
���� ���⿼��ֱ������Բ��λ�ù�ϵ��Ӧ�ã��㵽ֱ�ߵľ��빫ʽ��Ӧ�ã�������������������������

| A�� | {x|-2��x��1} | B�� | {x|-2��x��2} | C�� | {x|1��x��2} | D�� | {x|x��2} |
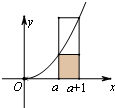 ��ͼ��ʾ����ֱ��x=a��x=a+1��a��0����y=x2��x��Χ�ɵ��������ε����������ӦС���������ε����֮�䣬��a2��${��}_{a}^{a+1}$x2dx����a+1��2�����֮��?n��N*��$\frac{1}{n+1}$+$\frac{1}{n+2}$+��+$\frac{1}{2n}$��A��$\frac{1}{n}$+$\frac{1}{n+1}$+��+$\frac{1}{2n-1}$���������ʵ��A���ڣ�������
��ͼ��ʾ����ֱ��x=a��x=a+1��a��0����y=x2��x��Χ�ɵ��������ε����������ӦС���������ε����֮�䣬��a2��${��}_{a}^{a+1}$x2dx����a+1��2�����֮��?n��N*��$\frac{1}{n+1}$+$\frac{1}{n+2}$+��+$\frac{1}{2n}$��A��$\frac{1}{n}$+$\frac{1}{n+1}$+��+$\frac{1}{2n-1}$���������ʵ��A���ڣ�������| A�� | $\frac{1}{2}$ | B�� | $\frac{3}{5}$ | C�� | ln2 | D�� | ln$\frac{5}{2}$ |
| A�� | �� m�Φ���n�Φ����� m��n | B�� | �����ͦã��¡ͦã��� ���Φ� | ||
| C�� | ��m�ͦ���n�ͦ����� m��n | D�� | �� m�Φ���m�Φ£��� ���Φ� |
 ��ͼ��������P-ABC�У�AC��BC��ƽ��PAC��ƽ��ABC��PA=PC=AC=2��BC=4��E��F�ֱ���PC��PB���е㣬��ƽ��AEF��ƽ��ABC�Ľ���Ϊֱ��l��
��ͼ��������P-ABC�У�AC��BC��ƽ��PAC��ƽ��ABC��PA=PC=AC=2��BC=4��E��F�ֱ���PC��PB���е㣬��ƽ��AEF��ƽ��ABC�Ľ���Ϊֱ��l��