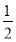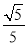题目内容
在△ABC中，角A，B，C对应的边分别是a，b，c.已知cos 2A－3cos(B＋C)＝1.
(1)求角A的大小；
(2)若△ABC的面积S＝5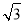
，b＝5，求sin Bsin C的值．
（1）
（2）
【解析】(1)由cos 2A－3cos(B＋C)＝1，得2cos2A＋3cos A－2＝0，
即(2cos A－1)(cos A＋2)＝0，解得cos A＝
或cos A＝－2(舍去)．
因为0<A<π，所以A＝，
(2)由S＝
bcsin A＝
bc·
＝
bc＝5
，得bc＝20.又b＝5，知c＝4.
由余弦定理，得a2＝b2＋c2－2bccos A＝25＋16－20＝21，故a＝
.
又由正弦定理得sin Bsin C＝
sin A·
sin A＝
sin2A＝
×
＝.
练习册系列答案
相关题目
