题目内容

已知f（x-2）=x²-4x，那么f（x）=

A.
x²-8x-4
B.
x²-x-4
C.
x²+8x
D.
x²-4

D
分析：利用求函数解析式的观察配凑法求解该问题是解决本题的关键，只需将已知的复合函数表达式的右端凑成关于x-2的表达式，再用x替换x-2即得所求的结果．
解答：由于f（x-2）=x²-4x=（x²-4x+4）-4=（x-2）²-4，
从而f（x）=x²-4．
故选D．
点评：本题考查学生的整体思想和换元意识，考查学生对复合函数的理解能力，做好这类问题的关键可以观察出表达式右端是自变量整体的何种表达式或者利用换元法转化解决，考查学生的运算整理能力．

练习册系列答案

自主假期作业本吉林大学出版社系列答案

高中新课程寒假作业系列答案

海淀黄冈寒假作业合肥工业大学出版社系列答案

寒假Happy假日系列答案

寒假成长乐园系列答案

寒假创新型自主学习第三学期寒假衔接系列答案

寒假创新性自主学习寒假突破系列答案

寒假高效作业系列答案

寒假假期集训系列答案

寒假接力棒系列答案

相关题目

5、已知f（x+1）=x²-x-2，则f（x）的解析式是（　　）

A、f（x）=x²+x-3

B、f（x）=x²+x+1

C、f（x）=x²-3x

D、f（x）=x²-3x-2

已知f 1(x)=|3x-1|，f2(x)=|a•3x-9|(a＞0)，x∈R，且f（x）=

f1(x)，f1(x)≤f2(x)

f2(x)，f1(x)＞f2(x)

（1）当a=1时，求f（x）的解析式；
（2）在（1）的条件下，若方程f（x）-m=0有4个不等的实根，求实数m的范围；
（3）当2≤a＜9时，设f（x）=f₂（x）所对应的自变量取值区间的长度为l（闭区间[m，n]的长度定义为n-m），试求l的最大值．

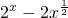已知f（x）是R上的偶函数，当x≥0时，f （x）= $数学公式$ ，又a是函数g （x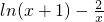）= $数学公式$ 的正零点，则f（-2），f（a），f（1.5）的大上关系是

A.
f（1.5）＜f（a）＜f（-2）
B.
f（-2）＜f（1.5）＜f（a）
C.
f（a）＜f（1.5）＜f（-2）
D.
f（1.5）＜f（-2）＜f（a）

已知f（x）是R上的增函数，点A（-2，1）、B（2，3）在它的图象上，那么，不等式|f^-1（x）|＜2的解集是（）
A．{x|-1＜x＜1}
B．{x|-2＜x＜2}
C．{x|-2＜x＜3}
D．{x|1＜x＜3}

已知f（x）是R上的增函数，点A（-2，1）、B（2，3）在它的图象上，那么，不等式|f^-1（x）|＜2的解集是（）
A．{x|-1＜x＜1}
B．{x|-2＜x＜2}
C．{x|-2＜x＜3}
D．{x|1＜x＜3}