题目内容
(满分14分)
已知函数
 是奇函数且满足
是奇函数且满足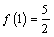 ,
, .
.
(Ⅰ)求 、
、 、
、 的值;
的值;
(Ⅱ)是判断函数 在
在 上的单调性并说明理由;
上的单调性并说明理由;
(Ⅲ)试求函数 在
在 上的最小值.
上的最小值.
【答案】
(Ⅰ) 
(Ⅱ)  ,函数
,函数 在
在 上为减函数
上为减函数
(Ⅲ) 函数 在
在 上的最小值为
上的最小值为
【解析】解:(1) 函数
函数 是奇函数,
是奇函数,
 ,即
,即  ,
, .由
.由 ,
, ,得
,得 ,
, ,解得
,解得 .
.

 ...........................4分
...........................4分
(2)由(1)得, ,
,  ,当
,当 时,
时, ,则
,则 .
.

 ,函数
,函数 在
在 上为减函数..................8分
上为减函数..................8分
(3)由 ,
, ,得
,得 .
. 当
当 时,
时, ,
,
 ,即函数
,即函数 在
在 上为增函数.又由(2)知
上为增函数.又由(2)知 处是函数的最小值点,
处是函数的最小值点,
即函数 在
在 上的最小值为
上的最小值为 ...............14分
...............14分

练习册系列答案
相关题目
 的前四项和为10,且
的前四项和为10,且 成等比数列
成等比数列
 ,求数列
,求数列 的前
的前 项和
项和
 的前四项和为14,且
的前四项和为14,且 恰为等比数列
恰为等比数列 的前三项。
的前三项。 的前n项和
的前n项和
 的前n项和为
的前n项和为 ,设
,设 ,求证:
,求证:
 的最小正周期为
的最小正周期为
 的单调递增区间;
的单调递增区间; 中,a、b、c分别是角A、B、C的对边,若
中,a、b、c分别是角A、B、C的对边,若 的面积为
的面积为 ,求a的值。
,求a的值。
 有三个零点
有三个零点 且
且 ,
, ,且
,且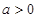 ,求函数
,求函数 试问:导函数
试问:导函数 在区间
在区间 内是否有零点,并说明理由;
内是否有零点,并说明理由; ,求
,求 的取值范围。
的取值范围。 的左、右焦点分别为F1、F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且
的左、右焦点分别为F1、F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且 的最小值不小于
的最小值不小于 。
。 ;
; 轴的右交点为Q,过点Q作斜率为
轴的右交点为Q,过点Q作斜率为 的直线
的直线 与椭圆相交于A、B两点,若OA⊥OB,求直线
与椭圆相交于A、B两点,若OA⊥OB,求直线